РУССКИЕ ЗОЛОТЫЕ САЖЕНИ. ЦЕЛОЕ И ЧАСТИ

                     Умом Россию не понять,
                     Аршином общим не измерить:
                     У ней особенная стать –
                     В Россию можно только верить.
                                                                                          Ф. И. Тютчев

                                             Нам не дано предугадать,
                                             Как слово наше отзовется, –
                                             И нам СО-ЧУВСТВИЕ дается,
                                             Как нам дается благодать…
                                                                                          Ф. И. Тютчев

Уже очень давно посетила меня догадка о том, что все известные, существовавшие ранее и существующие сейчас системы измерения есть части Системы Русских Золотых саженей, на протяжении пространств и в проистекании времен забывшие свои истоки.

О многих из них сейчас сохранились только отрывочные сведения, другие, как, например, английская, живут и здравствуют, третьи – восстановлены старанием и участием заинтересованных лиц.

Но мы вначале поговорим о метре.
Цитаты из общедоступных источников:
«Метр (русское обозначение: м; международное: m; от др.-греч. μέτρον – мера, измеритель) – единица измерения длины и расстояния в Международной системе единиц (СИ), одна из семи основных единиц СИ. Метр равен расстоянию, которое проходит свет в вакууме за промежуток времени, равный 1/299 792 458 секунды».

Более ранние определения метра:
«…В 1790 году (8 мая 1790, Французское Национальное собрание) метр получил следующее определение: — как длина маятника с полупериодом колебаний на широте 45° (примерно между Бордо и Греноблем), равным 1 секунде (в современных единицах это длина, приблизительно равная 0,994 м)».
«…В 1791 году вместо метода секундного маятника комиссия – среди членов которой были Жозеф Луи Лагранж, Пьер-Симон Лаплас, Гаспор Монж и Кондорсе – решила, что новая единица измерения должна быть равна одной десятимиллионной расстояния от Северного полюса до экватора (четверть земной окружности), измеренного вдоль меридиана, проходящего через Париж.
30 марта 1791 предложение определить метр через длину меридиана было принято: – как одна сорокамиллионная часть Парижского меридиана (то есть одна десятимиллионная часть расстояния от северного полюса до экватора по поверхности земного эллипсоида на долготе Парижа).
Интересно, что в современных единицах это 1/1,000 000 000 050 метра. Идея привязать единицу измерения длины к меридиану была не нова: аналогичным образом ранее были определены морская миля и лье».

Все выглядит внешне научно и убедительно, но не создается ли впечатление, что это наукообразие – всего лишь ширма, скрывающая имперские амбиции сильной тогда Франции? В современном мире все – идеология, все – политика. В том числе и единицы измерения…

Так чему же все-таки равен метр? Будем рассматривать методы определения длины метра по порядку, так как они возникли исторически.

1. Цитата 1: «Идея Уилкинса состояла в том, чтобы выбрать для единицы длины длину маятника с полупериодом колебаний равным 1 с. Подобные маятники были не так давно продемонстрированы Христианом Гюйгенсом, и их длина была весьма близка к длине современного метра (так же, как к длинам, использовавшимся в те времена, например, ярду)».

Все-таки, мы определяем длину 1 метра или длину 1 ярда?

Цитата 2: «Однако, вскоре было обнаружено, что длина, измеренная таким способом, различается в зависимости от места измерений. Французский астроном Жан Рише во время экспедиции в Южную Америку (1671—1673) обнаружил увеличение периода колебаний секундного маятника по сравнению с тем, который наблюдался в Париже. Выверенный в Париже маятник в процессе наблюдений им был сокращен на ¼ линий (2,8 мм), дабы избежать отставания во времени на 2 минуты в день. Это было первое прямое доказательство уменьшения силы тяжести по мере приближения к экватору, и это дало разницу в 0,3 % длины между Кайенной (во французской Гвиане)

Система русских золотых саженей / Блог архитектора Д. Новикова

В этой статье я хочу коснуться темы русских саженей — древней системы соизмерения. Если говорить об архитектуре, то эта тема является неизмеримо важной. Можно сказать, что она является краеугольным камнем архитектуры, как сакральной науки в практическом смысле. Все чаще и чаще в научной литературе отмечается плодотворное влияние на человека конструкций, пропорционированных по золотому сечению. Причём, имеются в виду любые конструкции и предметы, созданные человеком. От примитивной ложки до грандиозного дворца. Становится ясно, что пропорционирование частей зданий и сооружений, соответствующее природным пропорциям и пропорциям человека, его восприятию действительности и ощущениям, является важнейшим фактором здорового функционирования человеческого организма. Но как вычислять «золотые» пропорции и размеры? Анализ абсолютно всех древних сооружений, начиная с египетских пирамид, показывает присутствие Золотой пропорции, и многовариантность её применения сбивает с толку. А самые свежие из уцелевших золотосечённых сооружений древнерусские церкви и храмы. Издавна и аж до 18-го века на Руси строили согласно золотым пропорциям. Только Пётр I положил конец беспорядку, приравняв казённую сажень (217,6см) к 7 английским футам (213,360 см). В 1835г. Николай I вообще запретил остальные сажени, а в 1924 г. была введена метрическая система. Чтобы понять утраченные  и забытые суть и смысл измерения в древнерусских саженях, придётся немного окунуться в математику и геометрию. Золотое сечение / золотая пропорция /. Давно установлено существование загадочного Золотого числа или «Золотой пропорции» Ф. Это число тесно связано с системой саженей. Практическое знакомство с Золотым сечением начинают с деления отрезка прямой в «золотой пропорции» с помощью циркуля и линейки. Из точки В восставляется перпендикуляр, равный половине АВ. Полученная точка С соединяется линией с точкой А. На полученной линии откладывается отрезок ВС, заканчивающийся точкой D. Отрезок AD переносится на прямую АВ. Полученная при этом точка Е делит отрезок АВ в соотношении золотой пропорции. Точное значение Ф находится математическим путём как корень квадратного уравнения х-х-1=0, получаемого при делении отрезка в крайнем и среднем отношениях, то есть в соотношении золотой пропорции: АЕ/АВ=ВЕ/АЕ=Ф Решение для числа Ф всего одно: Ф=(1 + √5)/2 =1,6180339887498948482045868343656 Правда, у вышеупомянутого квадратного уравнения есть ещё один корень (1- √5)/2 = -1/Ф, но поскольку он отрицательный, это решение отбрасываем. Ф-число иррациональное бесконечное. Обратная величина  1/Ф=0,6180339887498948482045868343656 Ф= 2,6180339887498948482045868343656 Все знаки после запятой одинаковые Вот загадочное число, не правда ли? Но это ещё не всё. Известный числовой ряд Фибоначчи , где каждый последующий член ряда равен сумме двух предыдущих, имеет вид: 1,2,3,5,8,13,21,34, 55, 89,… 377, 610, 987,1598, 2885,… Нетрудно заметить, что с увеличением порядковых номеров членов деление последующего члена на предыдущий всё более приближается к золотому числу Ф:  3/2=1,5; 5/3=1,666; 21/13=1,615; 55/34=1,617; …610/377= 1,618037… Золотое иррациональное число Ф было известно еще в Древней Греции как основа образования бесконечного ряда величин, обладающего свойствами чисел Фибоначчи, получаемых в результате умножения или деления базисной единицы 1 на золотое число Ф. Ветвь ряда, образуемая последовательным умножением на Ф, называется восходящей: 1; 1,618; 2,618; 4,236; 6,854; 11,090; 17,944; 29,034 … а другая часть ряда, образуемая последовательным делением на Ф, называется нисходящей: 1; 0,618; 0,382; 0,236; 0,146; 0,090; 0,056; 0,034 …  Само число 1, первые три члена восходящего ряда и семь членов ряда нисходящего составляют греческий ряд чисел, получивших название « золотая пропорция» или «золотое сечение«. Итак, загадочное число Ф вычислено. Но зачем оно нам понадобилось? Оказывается, всё в природе, включая человека, создано согласно пропорциям золотого сечения. Мы любим красоту. Наше тело интуитивно чувствует золотую пропорцию. Всё, что нам кажется красивым, обладает свойствами золотого сечения. Будь то природный ландшафт, картина художника или тело человека. Почему это так, пока однозначного ответа нет. За последние десятилетия многочисленными исследователями были установлены повсеместные проявления закона золотых пропорций от Космоса до Микромира. Во Вселенной все известные человечеству галактики существуют в форме спирали, соответствующей формуле золотого сечения. Русский астроном Бутусов в 1978 г. установил, что отношение периодов обращения соседних планет вокруг Солнца равны либо золотой пропорции 1,618, либо ее квадрату 2,618. Соотношения золотой пропорции исследователи находят в морфологической структуре растений, птиц, животных, человека. Закономерности золотой пропорции обнаруживаются и в организации неорганической природы, например, структура талой воды, практически соответствует треугольнику золотой пропорции. Таким образом, проявление принципа золотых пропорций наблюдается повсеместно в природе от бесконечно больших галактик до бесконечно малых клеток и атомов. Фигура человека, исследованная немецким исследователем проф. Цейзингом в 1855 г. явилась ярким примером золотых пропорций. Дальше познакомимся с понятием вурфных соотношений. Для блока, состоящего из трех элементов с длинами а, b, c вурфное отношение W(а, b, с) вычисляется по формуле: W(a,b,с)=(а+b)(b+с)/b(a+b+с). При этом другой блок с другими размерами и другими соотношениями элементов а’, b’, с’ будет ему конформно симметричен, если величины их вурфов будут равны, т.е. если: W(a, b, с)=W(a’, b’,с’). Путем преобразований такие блоки могут быть совмещены один с другим с полным совпадением всех их точек. В процессе роста размеры частей тела человека и их соотношения все время меняются. Причём, эти изменения следуют принципам конформно-симметричных преобразований. Например, если взять соотношения стопы, голени и бедра в возрасте 1 года, 10 и 20 лет, то изменения выглядят так: 1:1,27:1,40;      1:1,34:1,55;     1:1,39:1,68. Рост различных частей тела не протекает равномерно. Голень и бедро увеличиваются значительно больше, нежели стопа, пропорции тела человека все время меняются. Вурфные же соотношения для любого возраста вычисляются с одним и тем же значением: W(1;1,27;1,40)=1,30;       W(1;1,34;1,55)=1,30;        W(1;1,39;1,68)=1,30 и оказываются неизменными на протяжении всего времени роста. Постоянная и неизменная величина вурфа свидетельствует о преобразовании форм нашего тела по принципам конформной симметрии. Такая же картина открывается и для других блоков: плеча предплечья кисти; фаланг пальцев; туловища, верхней и нижней конечностей тела и т.д. Значения вурфов немного варьируются, составляя в среднем величину W = 1,31. В идеальном случае В.Петухов указывает W = 1,309, что при выражении через величину золотого сечения равно Ф/2 . Он называет его « золотым вурфом» . Вурфные пропорции позволяют, следовательно, выявить конформно-симметричные группы, иными словами, группы родственных отношений с единым исходным началом. Обычные двучленные пропорции показывают лишь различия, вурфные общность некоторого множества трехчленных соотношений. Если пропорции окружающих нас произведений архитектуры, принадлежат к случайным группам, как в большинстве современных сооружений, то человек оказывается в среде, пропорциональная структура которой по своей симметрии ему не свойственна. Такая Среда, не обладающая ни одной из характеристических групп симметрии человека, чаще всего не воспринимается им, а нередко отвергается. Значительный прорыв в расшифровке древнерусских саженей произошёл, когда в Новгороде у церкви Параскевы Пятницы был найден обломок мерила новгородского зодчего. В процессе исследований мерила сначала Пилецкому А.А., а потом Черняеву А.Ф., удалось не только восстановить его полностью, но и показать, что оно являлось одновременно измерительным и соизмерительным инструментом. На одной грани были нанесены мерки всех саженей, а остальные три грани в комплексе с первой представляли собой своеобразную логарифмическую линейку, позволяющую очень просто подбирать золотые пропорции! Заодно были вычислены недостающие сажени и уточнены размеры известных. Список саженей приведён ниже. Многие названия восстановить не удалось, многие имели по нескольку названий, поэтому придуманы новые или использовано одно из старых названий. Также существовали более мелкие измерительные величины: полсажени (1/2 сажени), локоть (1/4 сажени), пядь (1/8 сажени), пясть (1/16 сажени), вершок (1/32 сажени). На основе саженей и их долей, а также последовательным умножением на 2 всех саженей, составлена матрица, названная Русский Всемер или «Русская матрица«: Оказалось, что все диагонали слева направо снизу вверх представляют собой ряды Фибоначчи и Золотую пропорцию одновременно. Для примера возьмём диагональ Народной сажени: 67,2+108,8=176,0         176/108,8=1,618              108,8/67,2=1,618 По строкам коэффициент везде 2/Ф = 2/1,618 = 1,236. Если расположить сажени в порядке возрастания длины, то соседние будут относиться друг к другу с одинаковым коэффициентом 1,059 так же, как частоты соседних полутонов в музыкальном ряду. Матрица может быть продолжена до бесконечности во все стороны — влево и вправо, вверх и вниз. Но матрицы такой в Древней Руси, очевидно, не знали, и более логично им было выбрать соответствие саженей размерам человека. Если принять народную сажень равной росту зодчего, то каждый мог пропорционально ей вычислить остальные сажени. Делалось это разными очень простыми методами, вообще без применения цифр и вычислений (геометрически). Видимо, со временем для удобства приняли единую саженную систему, ориентированную на рост среднего человека 176см, ему приравняли сажень народную. Читать продолжение ► Сажени # часть 2 Источник: masterkosta.com

Древнерусский Всемер. Факты подтверждают, что древнерусская мерная система сажени являлась общемировой

Наши предки обладали такими знаниями, от которых сегодняшняя «цивилизация» Земли непередаваемо далека. Да, в это трудно поверить, а ещё труднее представить, но это именно так и есть. Доказательства в тексте ниже…

 

Таблица размеров саженей. Древнерусский Всемер. Фото: http://alchalet.ru/

Нас всё время пытаются убедить, что Русь «образовалась» тысячу лет назад при крещении, что мы такие примитивные, «варвары, говорящие непонятно на каком языке…», и всё, чего мы достигли, всё это благодаря только более древним цивилизациям: египетской, греческой и европейской. К сожалению, эту точку зрения проводят в жизнь отечественные «горе-историки»,придерживающиеся до сих пор норманнской и других прозападных теорий происхождения Руси.

Нас убеждают, что и строить нас, опять-таки, научили греки, итальянцы и иже с ними. Однако огромное количество фактов и проведённый анализ показал, что в древнерусском «Всемере» были заложены знания, использовавшиеся не только русскими зодчими, но и зодчими других народов. Эти знания несли в себе глубокую информацию о гармонии мироздании, отражённую в числах.

Мерило

Полна загадок история Древней Руси. Но одно из самых загадочных её достижений – измерительная система, использовавшаяся при строительстве храмов и всех других сооружений. Сохранившиеся памятники архитектуры демонстрируют гармонию, как в эстетическом, так и архитектурном содержании. При этом утверждается, что-де церковная сажень имеет в основе древнеримские пассы, греческая – греческие оргии, великая сажень – шведский межевой локоть, а царская – египетский царский локоть… Иными словами, славянский народ якобы был не способен ввести единый измерительный инструмент и потому бессознательно собирал и использовал знания, наработанные соседними народами. С этих позиций даже предположение о возможности существования строгой пропорциональной системы древнерусских саженей представляется просто невероятным.

Однако видному архитектору А. Пилецкому удалось получить схему, названную им «Древнерусским Всемером», отображающую системную зависимость между саженями Древней Руси. Это своего рода числовая матрица, важнейшая особенность которой заключается в том, что она впервые показала глубинную суть древнерусских саженей, имеющих в основе золотую пропорцию!

Известно, что на Руси основным измерительным инструментом была сажень. Их существовало несколько десятков. Наиболее распространенными были – городовая (284,8 см.), великая косая сажень (249,6 см.), великая (244,0 см.), греческая (230,4 см.), казённая (217,6 см.), косая сажень (216 см.), царская (197,4 см.), церковная (186,4 см.), морская сажень (183 см.), народная (176,0 см.), кладочная (159,7 см.), простая (150,8 см.), малая (142,4 см.) и другие (Черняев А.Ф. «Золото Древней Руси. Русская матрица – основа золотых пропорций». М., 1998 г.).

Причём, сажень не являлась директивным неизменяемым инструментом, любой мастер мог изобрести свою персональную сажень. Зодчий в своей практике, как правило, пользовался набором из трёх-пяти саженей. Для измерения длины, ширины и высоты пользовались разными саженями. При измерении или строительстве одного и того же объекта могли пользоваться разными, несоразмерными друг другу саженями. Но главное было в том, что эти сажени должны были придерживаться строгой пропорции, а фактически соразмерны пропорциям Земли (её расстояниям от её центра до полюсов, до экватора и т.д. пропорции сооружения чётное число раз пропорциональны объёму Земли.

В качестве основного инструмента, по мнению академика Б.А. Рыбакова, для расчёта и измерения при проектировании и строительстве на Руси пользовались «мерилом» (фото обломка Новгородского мерила см. ниже), представляющим собой два плотно складывающихся бруска с нанесёнными на их трёх гранях рисками, т.е. некое подобие логарифмической линейки (рис. 1). Такой инструмент был найден при раскопках в Новгороде. Числа, вероятно, остались на утраченной части облома. А потому методика применения мерила остаётся не совсем ясной…

На одном мериле три разные шкалы, и, по мнению академика Б.А.Рыбакова, это означает, что перед нами – расчётный архитектурный инструмент, аналогичный логарифмической линейке. А каждая его шкала, видимо, пропорциональна какой-то сажени. Он стал разбираться и выяснил: сумма длин клеток на каждой стороне мерила оказывается равной городовой сажени (284,8 см). Причём на мериле «укладывались» размеры всех 14 саженей «Всемера». Рыбаков восстанавливает новгородское мерило в виде стержня, содержащего элементы набора частей длин трёх саженей: мерной (маховой), великой (косой) и прямой (простой), но в необычном для древнерусских пропорций делении – каждая сажень делится на 21 элемент

Согласно Б.А. Рыбакову, это необычное деление даёт древнему зодчему возможность оперировать элементами каждой сажени для воспроизводства архитектурных деталей и сооружений кругового очертания. Поскольку при любом диаметре круга, когда диаметр делится на 21 часть, в самом круге с большой точностью будут укладываться 66 таких же отрезков. Это деление известно с древности, как отношение Архимеда в виде пропорции 22:7 = 3,1428, что и обусловливает возможность построения любой окружности с точностью до 0,05% и проведения операции перевода окружности и отрезка любой окружности (дуги) в линейные меры.

Конечно, мерилом могли пользоваться только посвящённые. При этом им нужно было знать, сколько и какие отрезки-клетки мерила сложить или вычесть, чтобы получить заданные пропорции или нужную сажень. В любом случае все размеры будущего сооружения подчинялись гармонии «золотого сечения». При строительстве культовых сооружений каждый его параметр измерялся тремя вариантами саженей.
Представим используемые сажени в виде убывающего ряда и найдём численные соотношения между ними, сведя их в Таблицу 1. Как видно из Таблицы 1, все сажени соотносятся друг с другом в соответствии с законами золотого сечения, золотого вурфа, через соответствующие коэффициенты 1,618 и 1,309. . И лишь некоторые из группы саженей несколько «нарушают» общий порядок (1,102 вместо 1,059; 1,187=1,309:1,102 вместо 1,236; 1,362=1,102х1,236 вместо 1,309), при этом находясь в пределах матрицы, но в других рядах.

Поскольку гармоничность является одним из свойств золотого сечения, а число 2 – октава темперированной музыкальной гаммы и образуется малыми секундами, то было сделано предположение, что малая секунда, равная 2, соответствует коэффициенту 1,05946…, является шагом по вертикали русской матрицы и обеспечивает ей музыкальную гармоничную структуру.

Введение метра в качестве единицы измерения, нарушило эти пропорции и гармонию в сооружениях. Теперь в сооружениях все размеры в плане стали параллельными или перпендикулярными друг другу. Такие помещения – мертвы. В старых сооружениях этого нет, т.к. длина и ширина измерялись разными саженями, а это приводило к тому, что в плане сооружения нарушалась симметрия, и всюду имелись живительные углы наклона. При изменении положения в таком помещении создавалось ощущение оживления углов, и помещение на глазах как бы меняло свои размеры.

Дело в том, что в таком помещении нет негативно-скрытой – стоячей волны потока первичных материй («Неоднородная Вселенная»), выкачивающей из человека энергию. Здесь проявляется эффект полостных структур, который открыл В.С. Гребенников. В помещениях с такой структурой меняется мерность в местах сужения и происходит изменение плотности потока первичных материй – как в линзах поток света. Интенсивность потоков оказывает влияние на самочувствие человека. Это ещё раз подтверждает ту мысль, что наши предки сохранили часть ведических знаний, которыми обладали славяне до последней планетарной катастрофы.

Древний зодчий, как отмечает академик Международной академии информатизации при ООН А.Ф. Черняев, при проектировании сооружений ничего не вычислял, т.к. в этом не было необходимости. Имея «Всемер», зодчий выбирал соизмеримость саженей по правилу групп, т.к. он знал, что только при следовании методике – канону – можно получить красивое сопряжение пропорций, гармонию. А пропорции не вычислялись, т.к. они изначально заложены в длины саженей (см. Табл. 1). Набор из нескольких саженей, выбранных по канону, всегда составляют пропорцию (1,618), кратную золотому числу. Причём, канон не зависел, ни от каких физических воздействий, в отличие от метра, длина эталона которого зависит от температуры и др. воздействий. Сажень в виде верёвки деформируется равномерно, поэтому пропорции остаются неизменными.

Все размеры саженей, кроме крайних, могут быть связаны, как показано ещё А.А. Пилецким, с габаритами человека следующей зависимостью:

Таблица 2. Рост человека

В числителе – размер в положении с поднятой рукой, в знаменателе – рост человека.

Очень маленький – 176 / 142,4

Маленький – 186,4 / 150,4

Ниже среднего – 197,4 / 159,7

Среднего – 205,5 / 166,3

Выше среднего – 217,6 / 176

Высокий – 230,4 / 186,4

Очень высокий – 244 / 197,4

Здесь коэффициент, связывающий граничные значения в интервале соответствующего роста человека равен 1,236, например: 230,4/186,4=1,236.

На протяжении многих веков отсутствие единого стандарта не мешало, а более того – способствовало возведению великолепных, эстетически пропорциональных природе сооружений ещё и потому, что в древнерусской архитектуре все членения были трёхчастными.

Почленные части трёхчастного деления тела (вурфа) образуют систему взаимного пропорционирования и потому оказываются неразделимыми. Надо отметить, что, например, в живой природе, в биологических телах, в строении тела человека трёхчастное деление наблюдается постоянно. Например: пальцы рук и ног имеют трёхфаланговое строение, руки – трёхчленистое (плечо-предплечье-кисть: в 20 лет: 32,3-24,5-18,8 см), такое же ноги (бедро-голень-стопа: 45,4-37,5-27,0 см. в масштабе размеров тела (в антропологии трёхчленность также различают: верхний отрезок – от макушки головы до основания шеи; средний отрезок, или туловище – от основания шеи до тазобедренного сочленения; нижний отрезок – от тазобедренного сочленения до конца пальцев ног: 25,3-51,8-109,9 см.). Численные соотношения между размерами тела, равные 1,309, называются золотым вурфом (Коробко В.И., Коробко Г.Н. «Золотая пропорция и человек». – М., 2002. 394 с., ISBN 5-93-93-130-5). Это можно видеть и в Табл. 1.

Вурфные пропорции позволяют выявить группы родственных отношений с единым исходным началом. Обычные двучленные пропорции показывают лишь различия, вурфные – общность некоторого множества трёхчленных соотношений.

И если конструкция имеет вурфное отношение трёхчленного деления, то, как бы ни перемещался наблюдатель относительно неё, угол зрения А, В и т. д. всегда будет иметь одно и то же значение вурфа, и движущийся наблюдатель будет воспринимать постоянно меняющуюся, остающуюся эстетически совершенной, гармоничную конструкцию.

Во времена Петра I русскую казённую сажень испортили, изменив её длину на 4,3 см, и уложив в неё семь английских футов.

В продолжение книги Черняев А.Ф. «Система древнерусских саженей. Принцип золотого сечения»: athunder — LiveJournal

Черняев А.Ф. в книге «Система древнерусских саженей. Принцип золотого сечения.» подробно рассказывает, каким образом подбирать размеры дома, чтобы он был более гармоничным. Черняев приводит таблицу древнерусских саженей

а также объясняет, как ею пользоваться. Таблица конечно довольно просто строится, но при этом довольно сложно понять, как в древние времена люди могли знать число Ф, вычислять корни и пр. Точнее обычным строители и зодчие в те времена вряд ли пользовались сложными формулами.

И здесь на помощь приходит Хузяхметов С.Х. со статьей «Золотая симметрия русских саженей». Картинки в его статье отлично показывают зависимости между саженями. Особенно впечатляет фрактальная структура.

Где:
.F9 = 1,618 = (1 + .V5)/2 Функция прямого золота
.F1 = 1,058 = Ф3/4 Функция динамического равновесия
.F3 = 1,171 = Ф2л/5 Функция дополнения Хеси — .RA
.F4 = 1,236 = .V5 -1 Функция двойного золота
.F5 = 1,309 = Ф2/2 Функция золотого Вурфа
.F6 = 1,382 = .V5At> Обратная .F3

Кроме того, интересно, что характер взаимообратимости функции золотой симметрии вполне соответствует формуле гармонического соответствия, высказанного Альберти о том, что между двумя величинами должна существовать третья, обладающая родственными связями, т.е. быть соразмерной величиной: средней арифметической, средней геометрической, средней гармонической, иными средними.

Между любыми двумя функциями золотой симметрии существует гармоническая связь, которая напрямую через формулы взаимообратимости выявляет третью, обладая как бы памятью воспроизведения своей связующей функции. Эта связующая обладая инвариантной характеристикой воспроизведения по отношению к любым другим, возрождает непрерывную цепочку гармонических связей, имеющих фрактальный характер воспроизведения через любые другие функции в силу информационной избыточности функции золотой симметрии.

Сажени. Древняя система мер. Часть 2

Продолжение части 1-ой

Действительно, прокатило.

Мастеров, умевших ПРИМЕНЯТЬ осколки древней системы строительства, в эпоху Петра оставалось не так уж много. Знание утрачивалось, искажалось – и тут нужно было либо целенаправленно искать способы его возрождения, либо переходить на линейные, единообразные стандарты. Власть выбрала второе. Это вполне логично.

Далее я решил показать логику самого исследования. Как и почему двигался, как рассуждал, как делались выводы. Кому скучно – безжалостно пропускаем авторский трёп.

Для меня лично интерес к вопросу пробудил Черняев – ещё в 90-е. Замечательный его расклад «квадрата» Рыбакова просто запал в душу. Красиво очень. Без малейшего стёба. Ребята сделали фантастическую вещь – ясно показали, что в древних саженях ЕСТЬ система, и что в этой системе присутствует Золотое сечение – ряды Фибоначчи. Сам пример, на котором они это сотворили – несколько спорен (чуть-чуть, «по краешкам», но придираться я сейчас не буду). В любом случае, работа блистательная и важная. Так в чём же её изъян? Основной изъян, с точки зрения зарвавшегося автора?

Черняев разбирает ЧАСТНЫЙ СЛУЧАЙ системы. Он не видит её целиком. Да, гармония там присутствует. Она и должна присутствовать во всей системе, в том числе и в ЧАСТНОМ СЛУЧАЕ. И ряды Фибоначчи там есть. И исследовать это можно бесконечно – как бесконечно можно составлять слова, к примеру, из двенадцати букв алфавита – и даже какие-то тексты получатся.

Понимаю, наглое заявление. Но что поделаешь – если за рамки плоского квадрата Черняев так и не ушёл. Ещё раз – со всем уважением к Рыбакову и Черняеву. Лично мне их работа помогла чрезвычайно. С самого начала была уверенность, что решение ЕСТЬ, поскольку наличие гармонии (хоть и фрагментарно) они уже продемонстрировали.

Опасаясь «колейности», я намеренно не пошёл по их пути.

Первое, что было исполнено автором в плане поиска древней системы – это поиск фигуры, на которой она могла бы базироваться. Пирамиды, икосаэдры, додекаэдры… Мне виделась некая объёмная хрень – полумагическая – ребрами, гранями, сторонами, высотами которой выступают сажени. Надежда была именно на ОБЪЁМ. Мол, квадрат Черняева плоский, объёмных фигур он не рассматривал (во всяком случае, ничего об этом не пишет), тут нас и ждёт счастье.

И, самое интересное, такая фигура нашлась довольно скоро.

Шикарная фигура. Восьмигранная пирамида, в основании которой лежат два пересечённых под углом 45 градусов квадрата, один из которых и есть квадрат Черняева. Все грани пирамиды, высота в точку пересечения диагоналей квадратов, стороны квадратов, диагонали квадратов – всё составляли целые сажени.

Ну, думаю, вот она. Или почти она, может, ещё чего добавить)))). Подробнее об этом здесь… https://cont.ws/@sahalara/5064… . Там и фото.

Но в результате и это оказался тоже частный случай естественной гармонии системы – только чуть более развёрнутый. То бишь – не система базируется на фигуре (как бы ни была она хороша), а фигура получается из отрезков системы, поскольку в их длинах уже заложена определённая гармония.

В общем, «геометрический» путь мы проехали. Это тупик.

Так-то автор ещё поисследовал там прямоугольные треугольники – по каждой сажени, общим числом в несколько сотен штук… Дело в том, что основа большинства крепёжных конструкций именно прямоугольные треугольники, и их грамотное сочетание имеет значение на практике… В нашем случае представляли интерес варианты, когда ВСЕ ТРИ стороны треугольника складываются из цельных саженей. То бишь – и гипотенуза, и оба катета. Подобная комбинаторика, предположительно, должна была навести на мысли о том, как практически РАБОТАЛА Древняя система саженей (и можно ли вообще работать с таким количеством). То бишь – каким именно инструментарием мог располагать русский зодчий и как применял его при строительстве. Направление изначально расценивалось как прикладное (практическое) и не предполагало выход на ОСНОВЫ Древней системы. Погружение в «треугольники» позволило «почувствовать» рабочую комбинаторику этого набора отрезков, «почувствовать» скрытую за этим гармонию, и – частично – восстановить алгоритмы, с которыми работали зодчие. То бишь, саму технологию строительства.

Направление отработало именно так, как предполагалось.

А вот в теорию попала ветка «Алгебры». Уж не знаю, насколько это правильно, но для себя я называю её именно так.

Итак, поехали. Дальше совсем скучное – и безумно интересное для тех, кто понимает))). Числовые ряды.

Массив исследования – это ОПОРНЫЕ сажени, критерий отбора которых показан выше. Их 14 штук.

«Алгебраическая модель».

Первое, что было исполнено – это попытка соотнести сажени друг с другом.

Везде получались различные дроби, явно неудобные для вопросов строительства. То бишь, не половина, не треть и не четверть. Единственным исключением стала пара «Городовая» и «Малая», где «Малая» меньше ровно вдвое. Но… Маловато, чтобы использовать комплект из 14 саженей.

Разумеется, просмотрел соотношения между соседними саженями. И тут обозначилась странная вещь: сразу несколько из них соотносились с «соседом» с одним и тем же коэффициентом. 1.059.

Напомню список.

1 «Городовая» 284.8

2 «Без названия первая» 258.4

3 «Великая косая» 248.9-249.46 Она же «Косовая»

4 «Великая» 244.0

5 «Греческая» 230.4

6 «Казённая» 216.0-217.6 Она же «Косая»

7 «Царская» 197.0-197.4 Она же «Без чети»

8 «Трубная» 186.4-187.08 Она же «Церковная»

9 «Морская» 183.0-183.35

10 «Мерная» 176.0-176.4 Она же «Маховая»

11 «Кладочная» 159.7

12 «Прямая» 150.8-152.8 Она же «Простая»

13 «Малая» 142.4

14 «Без названия вторая» 134.5

Итак: «Городовая» к «Без названия первая» 1.102

«Без названия первая» к «Великая косая» в интервале 1.038-1.036

«Великая косая» к «Великая» в интервале 1.020-1023

«Великая» к «Греческая» 1.059

«Греческая» к «Казённая» в интервале 1.059 – 1.067

«Казённая» к «Царская» в интервале 1.094-1.105

«Царская» к «Трубная» в интервале 1.053-1.059

«Трубная» к «Морская» в интервале 1.017-1.022

«Морская» к «Мерной» в интервале 1.037-1.042

«Мерная» к «Кладочной» в интервале 1.102-1.104

«Кладочная» к «Прямой» в интервале 1.045-1.059

«Прямая» к «Малой» в интервале 1.059-1.073

«Малая» к «Без названия вторая»1.059

Несложно заметить, что из наших соотношений однозначны всего три. Остальные попадают в небольшой интервал – что связано с допусками саженей. Но два из трёх коэффициентов совпадают, и это же соотношение встречается в четырёх интервалов – то бишь, всего совпадений ШЕСТЬ. Это чудовищно много для 13 пар, и маловероятно (ОЧЕНЬ маловероятно) для случайности. Начинаем исследовать это соотношение в поисках гармонии.

Различные тупиковые версии (привязку к окружности, к какой-то правильной дроби, геометрической фигуре и прочее – опущу, поскольку они не подтвердились).

Зато прекрасно зарекомендовал себя числовой ряд – с коэффициентом 1.059.

Смотрим на него.

1

1.059

1.121

1.188

1.258

1.332

1.410

1.494

1.582

1.675

1.774

1.879

1.990

Ряд, что называется, шикарный. На двенадцатом шаге он почти точно выводит любую стартовую величину на удвоение. Погрешность десять промилле – это погрешность округления. Где-то что-то сбилось на миллиметр – но изначально должно было давать ТОЧНОЕ удвоение. Пока что это предположение, но предположение уже рабочее. Чем хороша такая раскладка степеней (с точки зрения практики)?

На пятом пункте (пятая степень) у нас 1.332. Это базовый размер плюс одна треть.

На седьмом пункте (седьмая степень) у нас 1.494. Это базовый размер полуторный.

На девятом пункте (девятая степень) у нас 1.676. Это базовый размер плюс две трети.

И на двенадцатом пункте (двенадцатая степень) у нас 1.990. Это удвоение базовой величины.

Разумеется, ряд можно продолжать – и на двадцать четвёртой степени базовая величина будет учетверена. При «обратном ходе» — если уменьшать с тем же коэффициентом – через двенадцать шагов она «ополовинится».

Кроме того, само количество шагов — 12 — уже красиво. По некоторым данным древняя система счёта не была десятиричной.

И это ЧРЕЗВЫЧАЙНО удобно для практических целей.

Измерять ничего не нужно, только отсчитал соответствующую сажень на связке.

Одно из неочевидных следствий – любой размер легко выражается при помощи этого ряда целыми его частями. Вообще любой. То бишь, бесконечные десятичные дроби в такой системе отсутствуют.

Второе неочевидное следствие – на шестом пункте (шестая степень) мы имеем ГИПОТЕНУЗУ равнобедренного треугольника базовой величины.

1 + 1 = 2, корень из двух 1.414, фактическое значение 1.410.

То бишь, можно брать базовую сажень (1) и шестую от неё по счёту – и это будут стороны квадрата и его диагональ. Точно также можно брать вторую по счёту сажень – и с ней соотносится седьмая, и опять это будут стороны квадрата и его диагональ, третью и восьмую – и так далее. Ряд бесконечен в обе стороны.

Имеет реальное значение для планирования квадратных помещений. Без лазера, шнуром диагонали выставлять хлопотно.

Фантастически удобно.

Маленький нюанс – сажени НЕ РАСКЛАДЫВАЮТСЯ в этот ряд. Фактически мы видим только несколько совпадений, подтверждающих КОЭФФИЦИЕНТ. И всё. Ряда пока нет, обрывки.

Продолжаем исследование.

Далее следует уточнить коэффициент. Согласно нашей гипотезе, он должен выводить на ТОЧНОЕ удвоение базовой величины. То бишь, вместо коэффициента 1.059 имеем какой-то другой, очень близкий, убирающий эту однопроцентную погрешность. Ищем его.

Это 1.05946

Именно он даёт ТОЧНОЕ удвоение базовой величины. Этот коэффициент АБСОЛЮТНО гармоничен.

Распишем его.

1

1.05946

1.12246

1.18920

1.25991

1.33482

1.41419

1.49828

1.58736

1.68175

1.78174

1.88769

1.99993

Погрешность убрана. Нас этот коэффициент устраивает больше, но насколько он сочетается с фактическими значениями саженей?

«Великая» 244.0 делим на 1.05946 – получаем 230.31

При фактическом значении «Греческой» 230.4

«Малая» 142.4 делим на 1.05946 – получаем 134.41

При фактическом значении «Без названия вторая» 134.5

Интервальные значения приводить не буду – соотношение НИГДЕ «не плывёт», поскольку уточнение было незначительным. Рабочее (пока) предположение подтверждается. Мы имеем новый, уточнённый коэффициент степенного (числового) ряда, с которым можно работать и смотреть, как на него ложатся фактические значения саженей.

Кстати, этот коэффициент – 1.05946 – это коэффициент Пифагора (1.0595) применительно к нотам, выводящий на октаву. Но об этом я узнал постфактум. Пока продолжаем искать.

В идеале – наши четырнадцать опорных саженей должны (вроде как) соответствовать этой пропорции – и выводить на удвоение (что мы и наблюдаем на примере «Малой» и «Городовой».

Впрочем, если бы всё было так очевидно, эту раскладку давно бы нашли. Фактически ситуация сложнее.

ПЕРВЫЙ ряд.

Начинаем с «Городовой», с наибольшей из 14 опорных саженей.

284.8 делим на 1.05946 – откладываем наш числовой ряд «в обратную сторону».

0. 284.8 «Городовая»

1. 268.83 такой сажени среди сохранившихся нет

2. 253.74 такой сажени среди сохранившихся нет

3. 239.50 такой сажени среди сохранившихся нет

4. 226.05 такой сажени среди сохранившихся нет

5. 213.36 такой сажени среди сохранившихся нет

6. 201.38 такой сажени среди сохранившихся нет

7. 190.09 такой сажени среди сохранившихся нет

8. 179.42 такой сажени среди сохранившихся нет

9. 169.35 такой сажени среди сохранившихся нет

10. 159.85 это «Кладочная» фактическое значение 159.7

11. 150.88 это «Прямая» фактическое значение в интервале 150.8-152.8

12. 142.41 это «Малая» фактическое значение 142.4

13. 134.42 это «Без названия вторая» фактическое значение 134.5

По идее, мы прошли на двенадцатом шаге «полный круг», «Малая» это половина от «Городовой». Но то, что дюжиной дело не ограничивалось – как и в нотах в инструментах не одна октава – видно по тому, что и дальше мы вышли на опорную сажень («Без названия вторая»).

Итак, мы прошли пространство наших 14 саженей, и имеем ПЯТЬ попаданий. Это ОЧЕНЬ много. Но продолжим.

Следующая сажень, от которой начинаем считать – «Без названия первая». Тот же коэффициент 1.05946

Это у нас ВТОРОЙ ряд.

1 258.4 «Без названия первая»

2 243.90 это «Великая» фактическое значение 244.0

3 230.21 это «Греческая» фактическое значение 230.4

4 217.29 это «Казённая» фактическое значение в интервале 216.0-217.6.

5 205.09 такой сажени среди сохранившихся нет

6 193.58 такой сажени среди сохранившихся нет

7 182.72 это «Морская» фактическое значение в интервале 183.0-183.35

8 172.46 такой сажени среди сохранившихся нет

9 162.79 такой сажени среди сохранившихся нет

10 153.65 такой сажени среди сохранившихся нет

11 145.03 такой сажени среди сохранившихся нет

12 136.89 такой сажени среди сохранившихся нет

И опять сажени закончились.

На этом числовом ряду также ПЯТЬ попаданий.

Два ряда с одинаковым коэффициентом «подобрали» 10 значений из 14.

Идём дальше. Следующая сажень, от которой начинаем откладывать числовой ряд – «Великая Косая», или «Косовая».

Это ТРЕТИЙ числовой ряд.

Значение «Косовой» находится в интервале 248.9 – 249.46. Тот же коэффициент – 1.05946

1. «Косовая» интервал 248.9 – 249.46

2. 234.93-235.46 такой сажени среди сохранившихся нет

3. 221.75-222.25 такой сажени среди сохранившихся нет

4. 209.30-209.78 такой сажени среди сохранившихся нет

5. 197.55-198.01 это «Царская» — фактическое значение 197.4

6. 186.46-186.89 это «Трубная», она же «Церковная», фактическое значение в интервале 186.4-187.08. Видно, как образовался этот интервал – одна погрешность потянула другую. Соответствуют именно ИНТЕРВАЛЫ.

7. 176.00-176.40 это «Мерная», она же «Маховая». Фактическое значение в интервале 176.0-176.4. И вновь такая же ситуация. Видно, как образовался интервал – он точно соответствует предыдущему.

Всё. Опорные (сохранившиеся) сажени закончились. На этом ряду у нас ЧЕТЫРЕ попадания.

Промежуточный вывод.

ВСЕ ЧЕТЫРНАДЦАТЬ опорных саженей лежат на одном и том же числовом ряду с коэффициентом 1.05946. Причём это гармонический коэффициент Пифагора.

Если кто-то способен трактовать это как случайно закрепившиеся в ремесле числа, «намеренные» разведёнными в стороны руками, ногами, али иными конечностями – я это комментировать не буду.

Но и это ещё не всё.

Коэффициент нашего ряда везде одинаков – 1.05946.

Но самих рядов ТРИ – и они никак друг с другом не пересекаются. Это для чего?

А посмотрим на эти ряды повнимательнее.

Коэффициент рядов Фибоначчи (золотого сечения), как известно, 0.618

Берём наш первый ряд, начинающийся с «Городовой», и умножаем его на 0.618.

0. «Городовая» 284.8 х 0.618 = 176.01 это «Мерная» из третьего ряда. (пункт семь)

Согласно свойствам числовых рядов второму пункту будет соответствовать восьмой, третьему – девятый и так далее. Оба числовых ряда точно соотносятся между собой через золотое сечение. ВСЕ ПУНКТЫ ДО ЕДИНОГО.

Берём второй ряд, начинающийся с «Без названия первая».

1. 258.4, «Без названия первая» х 0.618 = 159.69 это «Кладочная» из первого ряда (пункт 11)

2. 243.9 «Великая» х 0.618 = 150.73 это «Прямая» из первого ряда (пункт 12)

3. 230.21 «Греческая» х 0618 = 142.27 это «Малая» из первого ряда (пункт 13)

4. 217.29 «Казённая» х 0.618 = 134.28 это «Без названия вторая» из первого ряда, (пункт 14).

Сохранившиеся сажени на этом закончились, но по свойствам ряда понятно, что каждому последующему пункту второго ряда через «Золотое сечение» соответствует сажень первого ряда. Из того, что сохранились именно ПАРЫ, понятно, что они ПРАКТИЧЕСКИ использовались.

Берём третий ряд, начинающийся с «Косовой».

«Косовая» 248.9-249.46 х 0.618 = 153.8-154.17 это не сохранившаяся сажень из второго ряда.

По опорным саженям подтверждения нет (их всё же всего 14, но математически ряды сочетаются блестяще).

Вывод. КАЖДЫЙ размер первого ряда, умноженный на «Золотое сечение», соответствует размеру третьего ряда. КАЖДЫЙ размер второго ряда, умноженный на «Золотое сечение», соответствует размеру первого ряда. И КАЖДЫЙ размер третьего ряда, умноженный на «Золотое сечение», соответствует размеру второго ряда.

Абсолютная гармония.

Разумеется, если мы будем ДЕЛИТЬ а не умножать – будет та же связка, только в обратную сторону.

Для лучшего обзора сведём эти значения в таблицу.

Значения саженей в ряду соотнесены друг с другом через коэффициент «Золотого сечения». Видно, как один ряд перетекает в другой. То бишь, по столбцам у нас – ВЕЗДЕ коэффициент 1.05946; по строкам – ВЕЗДЕ коэффициент 0.618.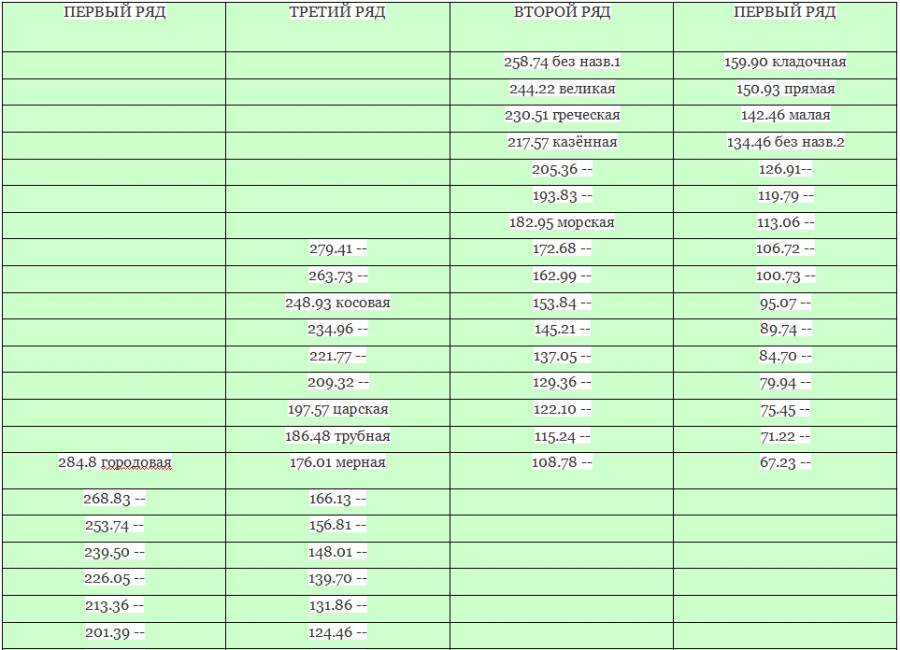

То бишь, на нижнее число 67.21 мы выходим как двигаясь вниз с коэффициентом деления 1.05946, так и вправо — с коэффициентом умножения 0.681.

И так — каждое значение ряда. И ВСЕ 14 сохранившихся саженей попадают в эту сетку!

Таблица считалась от сажени «Городовая», МАКСИМАЛЬНАЯ погрешность составила ОДНУ ТЫСЯЧНУЮ.

Напомню, свойства САМОГО РЯДА (перечисленные выше) позволяли зодчему работать с отрезками без измерений, просто отсчитывая их из комплекта.

А свойства ТРЁХ рядов, смещённых друг относительно друга, но сохраняющих единую пропорцию саженей, позволяли закладывать «Золотое сечение» прямо в размеры здания. Для этого достаточно было задействовать сажени из разных рядов, разных комплектов.

Кстати, ещё из этой последовательности замечательно выстраиваются купола – простыми треугольниками. Но это уже детали применения.

ВСЁ.

Может возникнуть возражение – мол, разложил рядами чуть ли не всё пространство, и все 14 саженей чудненько в него улеглись. Просто совпало. Там ведь допуски, все дела. Проверим математически вероятность этого «совпадения».

Интервал «Саженей» у нас охватывает пространство от 134.5 до 284.8

Это 151 сантиметр «пространства саженей».

Из первого ряда в нём у нас 14 точек; из второго 13; из третьего 14. Всего 41 точка.

Возьмём МАКСИМАЛЬНОЕ фактическое отклонение в одну тысячную (см.таблицу выше). Возьмём «среднюю» сажень – «Царскую», она же «Без чети». С учётом заданной погрешности это будет отрезок (интервал) в 4мм. (В примере «Царской» он как раз соответствует допустимой погрешности сажени). Таким образом, у нас (примерно) – 41 интервал по 4 мм.

Общее пространство саженей у нас 285 – 134 = 151 см = 1510 мм. Из них 164 мм «охвачено сеткой» числовых рядов. (41х4=164).

Предположим, что в реале сажени хаотично разбрасывались по всему отрезку – «ладошками» фиксировались. Именно это нам втирает официальная версия. Тогда они будут хаотично разбросаны по всему отрезку в 1510 мм, то попадая в нашу сетку, то не попадая. Итак, считаем шансы «случайности».

Вероятность того, что первая сажень попадает в сетку – 100 процентов, поскольку мы начинаем считать эту сетку именно с неё.

После чего у нас остаётся 13 саженей и оба интервала уменьшаются на 4 мм. (Один отрезок «выбит»).

Вероятность того, что вторая сажень попадёт в сетку – 160\1506=0.106

Вероятность того, что третья сажень попадёт в сетку при уже попавшей второй и первой 156\1502=0.104

Вероятность того, что четвёртая сажень попадёт в сетку при уже попавших в неё первой, второй и третьей 152\1498=0.101

И так далее. Не будем избыточно точны – пусть вероятность каждого последующего попадания уменьшается на две тысячных (на самом деле больше). Даже такой расчёт показывает нам общую вероятность «совпадения» для ВСЕХ ЧЕТЫРНАДЦАТИ ОПОРНЫХ САЖЕНЕЙ. Это 1х0.106х0.104х0.102х0.1х0.098х0.096х0.094х0.092х0.09х0.088х0.086х0.084х0.082.

Это дробь, на которой у меня «закончился калькулятор». Там двенадцать нулей до первого знака.

Вот теперь всё.

Эта таблица – и есть гармоничная система древних зодчих, остатки которой дошли до нас в виде сохранившихся саженей.

Три числовых ряда с одинаковым коэффициентом 1.05946, смещённые друг относительно друга на коэффициент «Золотого сечения» 0.618

Иначе говоря, любая из 14 сохранившихся саженей переводится в любую другую из этих же 14 при помощи коэффициента Пифагора 1.05946 (либо делением, либо умножением, смотря больше — или меньше). При этом часть из них нужно ещё дополнительно один раз умножить — или поделить — на коэффициент Золотого сечения. С точностью более одной ТЫСЯЧНОЙ — даже если операции умножения приходится проделывать несколько раз (там до 12 шагов получается).

Золотая Система саженей — Проявление Изначала — ЖЖ

А. А. Пилецкий и А. Ф. Черняев первыми показали, что сажени зодчих Древней Руси не случайно выбранные, надерганные откуда ни попадя величины, а стройная система, имеющая в своей основе пропорционирование по золотому числу Фи.

А. Ф. Черняев совершенно прав, говоря, что открытие А. А. Пилецким золотого пропорционирования саженей есть важнейшее архитектурное открытие ХХ века. От себя хочу добавить, что не только ХХ века, так как это открытие имеет вневременное значение. Это одно из тех открытий-озарений, которое рассеивает завесу, скрывающую от нас основополагающие законы развития Земли, Вселенной, Материи.

Опираясь на системность взаимосвязи различных саженей, А. Ф. Черняев проявил поле матрицы, которую назвал Русской матрицей.

Я вначале тоже пошла по этой же дороге. Но чем дольше я бродила по полю Русской матрицы, вникая в ее систему и вслушиваясь в созвучие чисел, тем явственнее мне грезилось нечто иное …

Неизвестно, сколько бы еще времени продолжались мои блуждания, но мой Путь привел меня в древний русский город Чухлому. Это – Костромская область, край, издревле известный своими мастерами и зодчими, отсюда строительные артели веками расходились-разъезжались по Руси и строили мастера, так, как «Мера и Красота велят» — по Золотому канону, переданному им их дедами-прадедами. И светлее становилось на Земле от этих творений. Как много они знали того, что сейчас сокрыто от нас во мраке времени! Казалось, навсегда утрачено их золотое мастерство. Их потомки строят как все – по метру и за деньги…

Уже не впервые была я здесь, снова жила одна в номере знакомой гостиницы, но в этот раз все шло по-другому… Стоял сентябрь, теплый, яркий, солнечный, а дела, по которым я приехала, почему-то никак не завершались… Что-то держало меня на этой древней земле, словно здесь хранилось то, что я давно ищу, и пришло время обрести желаемое.

Со мной были мои вопросы, мое желание и несколько избранных страниц из книги А. Ф. Черняева «Золото Древней Руси».

Город Чухлома находится на берегу древнего озера. Вода – проводник и хранитель информации на Земле. Сколько же ее накопила эта неподвижная, но живая вода! Сколько озарений, пониманий, знаний и умений стекли в озеро ручьями, дождями, упали росой и поднялись из глубин Земли живой ключевой, родниковой водой! Живое хранилище бесценной информации, вот оно, плещется светлой волной, и я каждый день прихожу к нему, брожу по его берегам, смотрю, как солнце и неторопливые облака отражаются в его водах.

Ни одно из пониманий и откровений, проявленных на Земле, не пропадает, не уходит бесследно, они остаются, как капли Света в энерго-информационном поле планеты, и могут быть востребованы каждым, чья чистота желания войдет в резонанс с их энергией, их вибрационно-частотными характеристиками. Мы получаем всегда ту информацию, до которой дотянулись чистотой своего желания, оформившегося в вопрос. Вот поэтому говорят, что вопрос всегда дается вместе с ответом.

Чистое Желание не имеет и не знает никаких границ и запретов, это истинный язык, который понимает все живое, суть взаимодействия с собой и с Миром. Мир, в котором мы живем, который чувствуем и воспринимаем, есть не что иное, как наше проявленное желание понять себя и измениться через это понимание. Мы все – творцы своих Миров и Вселенных, ведомые своим Желанием Изменения, которое так и называется – ЖИЗНЬ. В едином созвучии, возникающем в момент выбора Чистого Желания, проявляется на Земле информационное поле Космического Единства Материи и открывается вновь все, что было сокрыто.

Гуляя по берегу озера, я начала чувствовать и осознавать дотоле скрытые связи, а ночью, в номере гостиницы, я вдруг просыпалась, и, склонившись при свете настольной лампы, над влекущим своей чистотой листом бумаги, считала и писала, соразмеряя проявленное с ответом, приходящим из глубины сердца. С каждым днем я все яснее видела систему, о которой хочу рассказать вам. Этот процесс проникновения в суть не закончился, он вечен, ибо то, что миг тому назад казалось истиной в последней инстанции, в следующий миг становится только ступенью на бесконечной лестнице восхождения к осознанию себя и мира, который является частью тебя в той же мере, в какой ты являешься частью мира.

Когда все начало становиться на свои места, моя первая мысль – как все просто! Удивительно, почему до этого не дошли ни А. А. Пилецкий, ни А. Ф. Черняев, ни А. Чернов. Они сделали гораздо больше, всю огромную подготовительную работу, которую предоставили мне как основу для дальнейшего движения. Опираясь на проявленные ими понимания, я просто сделала следующий шаг.

Итак, Система древнерусских саженей, как я ее увидела. Что предполагается, когда говорится о любой системе? Прежде всего – взаимосвязанность и взаимообусловленность элементов, или иными словами – взаимодействие элементов по определенным объективным законам, то есть, зная ОДИН элемент системы, мы имеем возможность найти все остальные – восстановить всю систему.. Система как Целое включает в себя части-элементы, и в тоже время она заключена в каждую из частей-элементов, ибо иначе как, зная только один элемент, мы смогли бы восстановить всю Систему-Целое?

Таблицу, которую мы сейчас построим, можно считать производной от матрицы А. А. Пилецкого. Расположим 15 известных саженей несколько по-другому – более проявив тройственность, о которой неоднократно говорил А. Ф. Черняев, ибо в этой отмеченной им тройственности в действительности сокрыто Триединство.

Итак, знакомые нам уже 3 группы с их производными до вершка – вниз и удвоенные значения саженей – вверх.

1 группа – меньшая, малая, простая, кладочная сажени;

2 группа – египетская, народная, трубная, царская, фараонова сажени;

3 группа – Пилецкого, казенная, греческая, великая, большая сажени.

Построим таблицу, заполнив значения элементов каждой из саженей: полусажень, локоть, пядь, пясть, вершок, и значения удвоенных саженей.

Кстати, достаточно понятно, что вверх наша таблица может расти бесконечно и вниз тоже – ибо что такое «сажень»? – это некоторое целое, включающее в себя вышеперечисленные элементы. Деление на 2 производится до вершка, до 1/32 части, потому что части, меньшие 1/32, – 1/64, 1/128, не оказывают качественного влияния на целое – сажень. Но за целое-сажень мы можем взять и другую величину – например, не 176 см, а 44 см или 352 см. Отношения останутся прежними, просто будем иметь элементы другой величины, для 44 см вершок будет 1,375 см, для 352 см – 11 см.

        Величины саженей, которые выбраны как базовые, выбраны таковыми потому, что они созвучны антропометрическим данным человека.

Суть Золотой системы саженей в том, что она настраивается на каждого конкретного человека. При этом именно ЧЕЛОВЕК ставится во главу угла, становится элементом, содержащим в себе Целое – всю Систему, весь Мир, и проявляющим это Целое.

Пятью саженями второй группы закрывается без разрывов множество данных: от роста человека 156,10 см (размах рук – 160,93 см) до роста 209,36 см (размах рук – 215,84 см). Почему – будет показано далее. Но согласитесь, от 156,10 см до 209,36 см – этот интервал практически охватывает все множество величин роста взрослых мужчин, если говорить о наших предках-праславянах и о нас, славянах. Почему важно – мужчин – об этом далее расскажу.

В действительности Золотая Система саженей не имеет вообще никаких ограничений. Если бы ее строили для себя слоны, волки, пчелы или вирусы – они взяли бы соразмерные их физическим размерам величины саженей из общей, бесконечно увеличивающейся через удвоение и уменьшающейся через деление на два Системы. Самое важное – это то, что формы слона, волка, пчелы, вируса, как и все многообразие форм на нашей планете, строятся по законам, проявленным Золотой Системой саженей.

В Таблице 1 «плюсами» и «минусами» — например, + 0,27 см, — показано, на сколько я изменила значения саженей по отношению к данным А. А. Пилецкого и А. Ф. Черняева, для того, чтобы соотношения между элементами, впервые проявленные А. Ф. Черняевым, выполнялись точно. Корректировки эти крайне незначительны и не превышают 0,1%.

Итак, величины саженей третьей группы соответствуют высоте, до которой достает человек, подняв руку вверх. Обозначим их множество А_3i .

Величины саженей второй группы соответствуют величине размаха рук человека в стороны. Обозначим их множество А_2i .

Величины саженей первой группы – расстояние от уровня плеч или основания шеи до земли. Обозначим их множество А_1i .

Все эти соотношения показаны на Мерном ангеле Живого квадрата.

Связь между элементами 1 и 2 групп и между элементами 2 и 3 групп выражается одним и тем же соотношением:

A_1i / A_2i = A_2i / A_3i = Фи/2 = 0,809…

или A_ki / A_(k+1)i = Фи/2, где k = 1, 2.

Часто встречается обратное соотношение в виде коэффициента 2/Фи = 1,236…

A_2i / A_1i = A_3i / A_2i = 2/Фи = 1,236…

или A_(k+1)i / A_ki = 2/Фи, где k = 1, 2.

Мы уже знаем, что элементы внутри всех групп подчинены зависимости:

A_1i+1 / A_1i = A_{2i +1} / A_2i = A_{3i +1} / A_3i = 1,059… = ¹²√ 2

Выразим ¹²√ 2 через Фи, то есть покажем, что эта величина является степенью золотого числа Фи.

1.) Из A_1i / A_2i = A_2i / A_3i = Фи/2, получаем A_1i = Фи/2 х A_2i (1)

2.) Из матрицы А. А. Пилецкого имеем пропорциональность Фи для элементов, лежащих на диагонали, идущей снизу вверх и слева направо, например, 230,5 / 142,4 = Фи.

Для нашей таблицы эта зависимость примет вид A_3(i+1) / A_1i = Фи, откуда следует

A_3(i+1) = Фи х A_{1i .}

Из A_3(i+1) / A_2(i+1) = 2/Фи следует A_3(i+1) = 2/Фи х A_2(i+1) ,
            из этого и предыдущего имеем Фи х A_1i = A_2(i+1) х 2/Фи; отсюда A_2(i+1) / A_1i = Фи²/2.

Подставим (1) в полученное выражение:

A_2(i+1) / (Фи/2 х A_2i) = Фи²/2,

A_2(i+1) / A_2i = Фи³/4,

но из правила соотношения между соседними членами одной группы имеем

A_2(i+1) / A_2i = ¹²√2, то есть К_г. = ¹²√2= Фи³/4.

Выразим через Фи число 2.

2 = (Фи³/4)¹²= Фи³⁶/2²⁴,

2 = ²⁵√ Фи³⁶.

Через Фи можно выразить любое число, которое принято считать натуральным.

Очень ин

РУССКАЯ МАТРИЦА — ОСНОВА ЗОЛОТЫХ ПРОПОРЦИЙ : i_mar_a — LiveJournal

ДРЕВНЕРУССКИЙ ВСЕМЕР

«Вавилон» русской меры

Геометрическая система древнеруссских саженей

ЗОЛОТО НЕБЕСНОГО СЧЕТА

Мы не устаем рассуждать о загадочной Атлантиде. Пытаемся понять истоки возникновения письменности Шумера. Нас не в меньшей мере занимает математическая астрономия майи. Да и не все свои тайны раскрыли древнеегипетские жрецы… И Древняя Русь — со своими тайнами. Одно из самых загадочных ее достижений — измерительная система…
Говорят, еще древних греков осенило — все видимое и осязаемое должно радовать глаз. Главное — соизмерить… Так появилось золотое сечение, мы узнали о золотых цифрах, пропорциях… И выяснилось: в этих «золотых» делах — цифры особенные. То, что творилось в пределах золотых пропорций, не только обладало высокими эстетическими качествами, но и благотворно влияло на человека… Но, оказывается, и наши далекие предки, живя по законам «золотых» отношений, так или иначе имели сакральную связь с храмом иудейского царя Соломона, вавилонским столпотворением, пирамидами Древнего Египта и сооружениями куда более древних цивилизаций. Речь идет о потаенных знаниях изначальной Руси, в сути которых — и святое, и прекрасное, и чудесное… И, Бог знает, что еще через нас откроется миру… Об этом беседуют основоположник новой русской механики, академик Международной академии информатизации при ООН, автор оригинальных книг «Тайны пирамиды Хефрена», «Большой сфинкс: знак беды», «Золото Древней Руси», «Неньютоновскоя механика», «Диалектика пространство», «Авиакатастрофы», «Камни падают в небо» Анатолий ЧЕРНЯЕВ и журналист Сергей КАЛЕНИКИН.

КОСМОС — ДЕЛО ТОНКОЕ

Це́рковь Покрова́ на Нерли́ 1165 год

— Анатолий Федорович, посмотришь на древнерусские постройки — глаз радуется и душа светится. А наши величавые монастыри, храмы, соборы! От них сама благость исходит. Словом, постройки прошлого на удивление соразмерны и гармоничны. Но каким же чудесным образом зодчие Древней Руси сотворили такую красоту, когда они понятия не имели о миллиметрах, сантиметрах, метрах! Как им удавалось совершать такого рода творения, не имея представления о дробях, корнях?.. В чем тут секрет?

— В саженях. В прошлом они и были основным измерительным инструментом на Руси. Среди основных — городовая, великая, греческая, казенная, царская, церковная, народная, кладочная, простая, малая, косая… Правда, некоторые сажени имели несколько названий.

— Так сколько же их было на Руси?

— О том никто толком не знает. Грубо говоря, существовало несколько десятков саженей, если не сотен. Ведь в каждой местности были свои — черниговские, московские, новгородские, владимирские… Да и любой знающий мастер мог изобрести не одну персональную сажень. Она не являлась директивно неизменным инструментом. Причем сажени имели не только разную длину, но и, что особенно необычно, они были несоразмерны друг другу, хотя и использовались при замере объектов одновременно!

— А зачем столько саженей для одного и того же замера? Явный нонсенс! Безо всякой головной боли можно обойтись одной, как обходится ныне весь мир одним метром.

— Метр — продукт исторического развития человека. Это — стандартизованный, исключительно измерительный инструмент. И больше он ни на что не годится. Во всяком случае, для соизмерения не пригоден. Метр не отражает объем нашей Планеты.

— Разве? А кубический метр?

— Та же картина. Наши математики исходят из того, что длина, ширина и высота являются одинаковыми. А система саженей создавалась для соизмерений. То есть у древних зодчих метр в длину не равнялся метру в высоту и метру в ширину. Если мы будем придерживаться этого правила — сохраним это неравенство, то получим пропорции сооружения, которые будут соразмерны пропорциям Земли.

— Что это значит?

— То, что пропорции полученного сооружения четное число раз будут пропорциональны объему Земли. Скажем, возведенный храм становится соизмерим с Планетой. А если использовать обычный метр, то наше сооружение будет с нею несоизмеримо.

— Выходит, сажень — явление космическое?

— Выходит, так. Но вернемся к метру. Считается, что измерительный инструмент должен с большой точностью делиться на некоторое количество одинаковых мерных единиц, обычно кратных круглому числу. Метр делится на десять дециметров, дециметр — на десять сантиметров… Сам по себе метр является стандартной величиной, десятимиллионной долей от одной четверти парижского меридиана. И получение его эталонной длины — достаточно сложная, продолжительная и дорогостоящая операция. Полученный эталонный метровый отрезок, в виде выверенного платинового стержня, уже почти 200 лет хранится в футляре при постоянных температуре, давлении и влажности. Но даже в этих условиях требуется уточнение его длины. Сажень имеет иную логику.

15,11 / 12,22 / 9,888 / 8,000 / 6,472 / 5,236 / 4,236
7,554 / 6,111 / 4,944 / 4,000 / 3,236 / 2,618 / 2,118
3,777 / 3,056 / 2,472 / 2,000 / 1,618 / 1,309 / 1,059
1,888 / 1,528 / 1,236 / 1,000 / 0,809 / 0,654 / 0,529
0,944 / 0,764 / 0,618 / 0,500 / 0,404 / 0,327 / 0,264
0,472 / 0,382 / 0,309 / 0,250 / 0,202 / 0,164 / 0,132
0,236 / 0,191 / 0,154 / 0,125 / 0,101 / 0,082 / 0,066

Фрагмент русской матрицы
В центре — единица. А по диагонали от нее слева направо и снизу вверх идет восходящая ветвь золотой пропорции. Главная диагональ пересекает вертикальный ряд чисел под углом 45 градусов, образуя вместе с другой диагональю, вертикальным и горизонтальным рядами фигуру двойного креста.

НЕ ОРГИИ, А ВСЕМЕР

— Как раз с логикой саженей не все понятно. Обилие различных видов, их диспропорциональность в единой кратности и несоразмерность каким-либо мерным инструментам вызывают недоумение. К тому же, насколько я понимаю, нет и единой минимальной единицы измерения для всех саженец. Кстати, откуда родом древнерусская измерительная система?

— Различные авторы по-разному определяют время ее возникновения. По мнению одних, большая часть саженей у славян образовалась в XII—XIII веках и развивалась примерно до XVII века. Некоторые считают, что она собрана с миру по нитке, «занесена на русскую равнину, вероятно, задолго до утверждения там славян, в III—II веках до Рождества Христова, из Пергама через малоазиатские греческие колонии». Кто-то полагает, что сажень привнесена в Древнюю Русь из других сопредельных или отдаленных стран.
Утверждается, что-де церковная сажень имеет в основе древнеримские пассы, греческая — греческие оргии, великая сажень — шведский межевой локоть, а царская — египетский царский локоть… Иными словами, славянский народ был не способен ввести единый измерительный инструмент и потому бессознательно собирал и диспропорционально использовал знания, наработанные соседними народами. С этих позиций даже предположение о возможности существования строгой пропорциональной системы древнерусских саженей представляется просто невероятным.
Однако видному архитектору А.Пилецкому удалось получить схему, отображающую системную зависимость между саженями Древней Руси. Используя ее, он пришел к построению системы пропорций, которую условно назвал «Древнерусским Всемером». Получилась своего рода числовая матрица. И ее важнейшая особенность заключается в том, что она впервые показала глубинную суть древнерусских саженей, которые, как оказалось, имеют золотую пропорцию!
Больше того, «Древнерусский Всемер» превращает отдельные — вроде бы не связанные между собой — измерительные инструменты определенной длины в систему соразмерных, пропорциональных «золоту» длин, образующих поле взаимосвязанных чисел — матрицу. Она и обусловливает числам органическую взаимосвязь всех саженей. Есть и другие особенности.
«Древнерусский Всемер» А.Пилецкого — важнейшее историческое, культурное и архитектурное открытие XX века в России. Мы восстановили необыкновенный инструмент. Он определяет весь процесс зодческого творчества древности. Этот инструмент позволяет получать принципиально новые (точнее — полностью утраченные) числовые взаимосвязи, отображающие пропорциональное «золоту» совмещение длин саженей.
Древнерусские сажени
(по А.Пилецкому)
в сантиметрах:

городовая — 284,8
без названия — 258,4
великая — 244,0
греческая — 230,4
казенная — 217,6
царская —197,4
церковная — 186,4
народная —176,0
кладочная —159,7
простая — 157,8
малая —142,4
без названия —134,5…

— То есть речь идет о кратности всех саженей золотому числу — 1,618?..

— Совершенно верно. И кратность всех саженей золотой пропорции однозначно демонстрирует надуманность всевозможных рассуждений о заимствовании каких бы то ни было случайных измерительных инструментов. Древнерусские зодчие необоснованных или случайных размеров не допускали.

— То, что пропорции золотого сечения отличаются исключительно высокими эстетическими качествами и определяют наивысшую соразмерность между целым и его частями, известно многим. Но спрашивается: откуда возникли представления о делении отрезков в крайнем и среднем отношениях, позволяющем получать золотое число и пропорцию, названную Леонардо да Винчи «золотым сечением»?

— Уже в Древней Греции на основе золотого числа посредством последовательного умножения и деления базисной единицы на число 1,618 получали ряд из 11 чисел, имеющий название «золотого ряда», бесконечного в обе стороны:

…; 0,034; 0,056; 0,090; 0,146; 0,236; 0,382; 0,618; 1,000; 1,618; 2,618; 4,236; …

Каждое число этого ряда представляет собой иррациональную — бесконечную — последовательность цифр, округленных до четырех знаков. Каково собственное значение этих чисел и к какой геометрии они относятся, также неизвестно, а потому числа эти стоят на обочине современных наук.

— Интересно, а как выглядел инструмент сажени в Древней Руси?

— В качестве «рулетки» или «метра» наши предки использовали металлический пояс. Но он мог быть и из ткани.

— Но ведь ткань деформировалась — растягивалась или по какой-то причине «усыхала»…

— Ну и что? Если пояс был заранее отмечен узлами, то он деформировался пропорционально. Но чаще всего пользовались деревянными инструментами. И в этом сажень качественно отличается от метра, который — статическая измерительная единица, эталон, предназначенный для сопоставления с собой всех измеряемых тел.
Сажень соразмеряет пропорции процессом. Он как бы оживляет их. Все, что движется, — живет и дышит соразмерно. И пропорции саженей подвижны. Их динамика подвигала истинного мастера на создание гармоничного объекта. И чем большей духовностью обладал мастер, чем тоньше его чувство возвышенного и возвышающего, тем более впечатляющим будет продукт его творчества. Потому сооружения Древней Руси и отличаются такой соразмерностью, пропорциональностью и эстетической красотой — с облагораживающим воздействием!

ЧТО ЕСТЬ ЖИВОЕ

— Эзотерика утверждает: числа и геометрические фигуры делятся на живые и неживые. Вы, в принципе, касаетесь этой же сферы.

— Минутку. С моей точки зрения, общим недостатком эзотерического подхода в этом вопросе является отсутствие однозначных критериев отличия живых чисел и фигур от аналогичных неживых. Насколько мне известно, в публикациях эзотериков не сообщается, какое качество, а быть может, качества способны придавать таким абстрактным понятиям, как число и геометрическая фигура, свойства, признаваемые за живыми и неживыми телами.

— Возможно. А каково ваше, Анатолий Федорович, понимание живого и неживого? По сути. Что вы, предположим, скажете о «живом квадрате» или…

— Коли бывали в храме, замечали, что у вас одно состояние, настроение — ощущение живого. А находясь в обычном — стандартном помещении, мы этого состояния не улавливаем. В чем тут дело? Вникнув, к примеру, в план церкви Успения в Старой Ладоге, увидим: что-то не так. Стенки храма почему-то «поехали» — относительно оси они явно сдвинуты. Лихая небрежность зодчего? Отнюдь.

Мерный Ангел живого квадрата на плане церкви Успения (Старая Ладога)

церковь Успения (Старая Ладога), фасад

Тут вот какая закавыка. Наше зрение настроено на восприятие объема, мы все равно, автоматически, стены видим под прямым углом. И находясь в помещении, построенном в русских саженях, мы видим, что помещение вроде бы строго квадратное. Однако если изменим положение тела, перекинув свой взгляд в иную точку, у нас все меняется! Нет былой симметричной строгости. То есть когда я двигаюсь, изменяется угол, но между тем суммарные пропорции угла помещения остаются неизменными. От движения глаз помещение не только оживает, но и на глазах меняет свои размеры — разумеется, для глаза.
В старых помещениях строгой параллельности никогда не было. Всюду имелись живительные углы наклона. Таковы архитектурные тонкости, и глаз непременно их улавливает. К тому же настрой идет от стен, которые возведены по тройным саженям. В таком помещении нет негативно-скрытой — стоячей волны, выкачивающей из человека энергию. А когда ее нет, сама конструкция помещения настраивает человека на благоприятный — благостный резонанс. С другой стороны, и сам человек в нормальном помещении своим колебанием возбуждает благодатный для себя резонанс.

— А откуда берется эта окаянная стоячая волна?

— Она возникает тогда, когда параметры помещения кратны какой-то величине. В строго параллельных, симметричных, а стало быть, мертвых помещениях. А по русским саженям — никакой кратности нет, ибо сами сажени ее не имеют. Они безразмерны. А о живом квадрате скажу так: это та переходная граница, отделяющая восприятие квадрата от прямоугольника. Или: это такая фигура, которая еще не квадрат, но уже и не прямоугольник. Живой квадрат имеет как бы подвижные грани, движение, а следовательно, живет. Он в подвижном состоянии. А неживое — неизменное, статичное, сплошь и рядом — убогая симметрия. Тут и речи нет о золотом сечении.

— Анатолии Федорович, а как зодчий Древней Руси вычислял золотые пропорции?

— Ничего он не вычислял. Он знать о них ничего не знал. Да и необходимости в том не было. Имея «Всемер», зодчий выбирал соизмеримость саженей по правилу групп. Видимо, древний мастер даже не представлял себе, что у кого-то можно что-то посчитать, измерить. Поскольку работал не соизмеримыми сантиметрами, а несоизмеримыми саженями. Но он хорошенько знал, что только при следовании методике — канону можно получить красивое сопряжение пропорций, гармонию. А пропорции не вычислялись, так как они изначально заложены в длины саженей. Набор из нескольких саженей, выбранных по канону, всегда составляет пропорцию, кратную золотому числу.

КТО БЕЗ СВЯТОСТИ, А КТО ОТ БОГА

— Спору нет: сажени — в золоте, прекрасны, гармоничны… Но все же сгинули они. А почему?

— Наша древняя измерительная система стала портиться со времен Петра, который русскую казенную сажень перевел в точной пропорции с английскими футами. Изначально она равнялась 217,6 сантиметра, но при Петре она сократилась до 213,3 сантиметра. В казенную сажень уложили семь английских футов. К началу XIX века только в церковном строительстве сохранилась исконная древнерусская саженная система. Сейчас же Церковь строит, как и все прочие, используя метрическую систему измерения. И святость сейчас в ней не закладывается.

— Вернемся к прошлому. И проясним: что прежде всего учитывалось при строительстве? Использовались ли древними мастерами при сооружении объектов какие-то особые принципы?

— Разумеется, и их было немало. Так, если мы сейчас все что угодно возводим от земли, то в прошлом, наоборот, любое сооружение строилось с высоты. От Бога! То есть прежде всего зодчий выяснял высоту, которая определялась от верха креста. А только потом задавались ширина и длина. Причем сакральный объект по высоте имел два размера: один — мирской, а другой — скрытый, сакральный.

— То есть одна и та же высота замерялась дважды разными саженями?

— Да, но при мирском варианте (для мирян) учитывалось четное количество каких-то саженей. Их могло быть 12, 14, 16 и так далее. А сакральная высота подразумевала стремление к Богу. И такая высота должна была иметь нечетное количество саженей, но при этом их кратность равнялась семи! Особенно важным для мастеров было отображение потаенной пропорции в композиции духовных сооружений. Скажем, церковь является храмом Божьим — храмом Христа, объектом святости для верующих и даже неверующих. Святость — мерило Церкви. А мерило всегда выражается числом. Числом, за которым может скрываться качество, в том числе и значимость возводимого объекта.
Семь — число Христа, священное, сакральное число. И качественная композиция сооружаемой церкви как храма Христа, как сооружения духовного в своей потаенной пропорции включала элементы сакральности, содержащие совмещенное количество сдвоенных мер: мирские, открытые для всех, и потаенные, кратные семи. Однако не посвященные в суть таинства христианства не замечали ни сдвоенности, ни кратности, как не замечали, что церковь имела не менее семи саженей различной длины.
Эти правила были настолько законспирированы и с такой осторожностью соблюдались, что и сегодня, любуясь, например. Великой Печерской церковью в Киеве, церковью Вознесения в Коломенском или той же церковью Параскевы Пятницы в Новгороде, даже крупные нынешние архитекторы не догадываются ни о двойной мерной структуре этих шедевров, ни и о саженной сакральности.

Церковь Вознесения (Коломенское), 1528 год

Церковь Параскевы-Пятницы в Новгороде, 1207 год

— Можете ли вы для ясности дать какие-то пояснения? В цифрах.

— При рассмотрении плана церкви Параскевы Пятницы выясняется, что ее длина равна 21,1 метра, или 12 саженей народных (по 1,76 м), а ширина — 18,1 метра, или 12 саженей простых (по 1,508 м). Эта информация указана в любом справочнике по древнерусской архитектуре. Но вот оказывается, что в длину укладывается также 14 саженей простых (семь сдвоенных саженей по 1,508 х 2) и семь саженей больших. Как видите, и здесь сакральность. И снова «Всемер». Вот и получается, что планы церквей с самого начала в потаенной форме содержали определенную мистерию сакральных чисел.
И не только церковь Параскевы Пятницы, но также, скажем, Великая Печерская церковь в Киеве, церковь Вознесения в Коломенском, церковь Спаса-на-Нередице в Новгороде возведены с учетом саженной системы «Всемера» А.Пилецкого. Стало быть, она была широко распространена по всей Руси и применялась примерно с X века — если судить только по вышеуказанным церквам.

церковь Спаса-на-Нередице в Новгороде, 1198 год

— Анатолий Федорович, неужто данные всех саженей «Всемера» древние хранили в памяти? В это, право, не очень-то верится. Наш мозг так не работает.

— Обычно хорошо запоминаются семь предметов (чисел) и их взаимосвязи. А «Всемер» вмещает в два раза больше, плюс сложное сочетание групп. Запомнить все это трудно. К тому же в своей повседневной практике зодчий пользовался в основном набором из трех — пяти саженей. О существовании прочих он со временем забывал. А потому надежная и секретная передача «Всемера» из поколения в поколение была возможна лишь в том случае, если он был зафиксирован на пусть даже относительно недолговечном — железном или деревянном — носителе.
…В 1970 году при раскопках в Новгороде, недалеко от церкви Параскевы Пятницы, в слоях начала XIII века были найдены части деревянного мерила. Облом мерила сохранился в виде двух четырехгранных еловых брусков размерами 28×36 мм в поперечнике и длиной 22 и 32 сантиметра, плотно складывающихся воедино. Три грани бруска размечены на клетки трех различных длин. Но облом заканчивается 13-й большой клеткой.

Осколок новгородского мерила

— А на шкалах мерила имеются какие-то цифры, знаки?

— В том-то и дело, что нет. Числа, вероятно, остались на утраченной части облома. А потому методика применения мерила остается не совсем ясной… На одном мериле три разные шкалы, и, по мнению академика Б.А.Рыбакова, это означает, что перед нами — расчетный архитектурный инструмент. А каждая его шкала, видимо, пропорциональна какой-то сажени. Стал разбираться и выяснил: сумма длин клеток на каждой стороне мерила оказывается равной городовой сажени (284,8 см). Причем на мериле «укладывались» размеры всех 14 саженей «Всемера» (кстати, их уникальная система соизмерима со всей совокупностью геометрических размеров Земли: расстояниями от ее центра до полюсов, до экватора и т.д.).
И как-то само собой мелькнула мысль: а вдруг новгородское мерило — древнейшая логарифмическая линейка? Во-первых, в этом мериле «сидят» все варианты русских саженей. Во-вторых, по линейке мы передвигаем цифры относительно друг друга. И нечто подобное наблюдаем в новгородском мериле.

— Но главного — числовых-то значений нет!

— Нет. Зато есть «цифровые» деления! Брусок делится на отрезки — на клетки. И значение имеет только их номер. Клетка представляется как некая единая величина. Она — своего рода квант. И отношение номеров квантов — клеток друг к другу определяет структуру всех создаваемых пропорций. Имейте нужную клетку — и у вас резко уменьшится количество операций по подбору пропорций каких-либо сооружений, строений. Поистине «золотое» дело древнерусского мастера сводилось к сложению и вычитанию номеров клеток мерила в определенной последовательности.
Короче говоря, облом мерила новгородского зодчего является частью инструмента, выполнявшего функции носителя «Всемера», или «логарифмической» линейки. Ею, конечно, владел не каждый, а только посвященные. Она была потаенным инструментом.

— Анатолий Федорович, с новгородской «логарифмической» линейкой как-то что-то ясно. Есть ли еще данные, свидетельства, подтверждающие древность русских саженей?

— Иерусалимский храм. Когда во главе народа иудейского стоял царь-праведник Давид, Господь передал ему через пророка Нафана такие слова: «Сын твой, которого Я посажу вместо тебя на престоле твоем, он построит дом имени Моему» (3 Цар. 5,5).
Прошло время, и на иудейский престол вступил сын Давида — царь Соломон. История на века сохранила свидетельства его мудрости. Однако от одного из самых главных творений царя — легендарного храма Иерусалимского ничего не осталось…
Это сооружение для того времени было колоссальным: высота — 16 метров, длина —43 метра, ширина — 21 метр [Определение размеров храма основано на Библии: «И построил он (Соломон) дом из дерева ливанского, длиною во сто локтей, шириною в пятьдесят локтей, а вышиною в тридцать локтей» (3 Цар. 7,2) — Ред.]. Все три числа в размерности метра несут в себе сакральную для христианской культуры цифру — 7 (16; 1 + 6 = 7; 43; 4+3 = 7; 7 х 3 = 21). За тысячу лет до рождения Христа этими числами было продемонстрировано знание той мерности, которой будут пользоваться люди три тысячи лет спустя.

— Но это уж чересчур вольное манипулирование цифрами…

— А древнерусские сажени? Тут открываются новые неожиданности: к примеру, каждый параметр Иерусалимского храма размерялся не двумя, а тремя вариантами саженей! А ведь тройственность — основа христианства, в данном случае свидетельствующая о Божественном Промысле в строительстве храма. Я не знаю других сооружений, которые размерялись бы разными инструментами трижды.
И еще вот что поразительно. При планировке Иерусалимского храма нашли применение семь разных, бытовавших впоследствии на Руси саженей. То есть зодчий храма имел под руками инструмент, подобный новгородскому мерилу. Кстати, о самом этом зодчем. Сведения о нем основаны не только на ветхозаветных преданиях, но и на таком весьма распространенном в средние века (в том числе в русском переводе) апокрифе, как «Сказание о Соломоне и Китоврасе». В роли зодчего там выступает Китоврас (так называли на Руси кентавра). Он в «Сказании» необыкновенно мудр. Соломон говорит Китоврасу: «Не на потребу тя приведох собе, но на упрос очертания святая святых» (то есть «чтобы вопросить о планировке святая святых», храма). И вот Китоврас явился к Соломону с деревянным мерилом длиною четыре локтя («умеря прут четыре локоть […] поверже прут царем молча»). Но и в Древей Руси каждая сажень подразделялась именно на четыре локтя! Так, может быть, Китоврас «Сказания» — вовсе не кентавр, а мастер из протославянских, проторусских земель? Опытный мастер, хранитель традиции, которой слышали тогда и в далекой Палестине…

Реконструкция Храма Соломона, выполненная французским исследователем Ш.Шилье (начало XX в.)

— Выходит, система измерительных инструментов, которую мы именуем древнеславянской, существовала еще до царя Соломона?

— Выходит… Египетские пирамиды возведены почти за 3000 лет до нашей эры. Они до сих пор остаются загадочными и по технологии возведения, и по тем знаниям, которыми владели строители пирамид. Одна из самых интригующих — загадка мерных инструментов, с помощью которых строили в Древнем Египте.
Возведение строго выверенных по своим геометрическим параметрам пирамид (практически точные углы 90 градусов, отклонение сторон основания всего на 2 — 3 сантиметра при длине более 200 метров, соблюдение до секунд углов наклона боковых сторон, сведение граней пирамид в одну точку на высоте более 100 метров и т.д.) свидетельствует о наличии у строителей точных измерительных инструментов и хорошо отработанной методики пространственного измерения. То, что в течение столетий археологи и ученые не могут определить величину древнеегипетского аналога современного метра, скорее всего свидетельствует об отсутствии единого мерного инструмента и о возможном существовании в Египте некоторого подобия древнерусской системы измерительных инструментов. И возникает вопрос, а не может ли оказаться так, что в Древнем Египте, и в Древней Руси использовалась одна и та же метрологическая система? Но ведь это так! Вычисления показывают: все помещения и объекты комплекса пирамид в Гизе проектировались и возводились по мерным инструментам, полностью соответствующим тем единицам измерения, которые мы называем древнерусскими саженями. К примеру, в структуре параметров пирамиды Хеопса мы находим десять вариантов древнерусских саженей.
Но и это не все. Еще более древние сооружения Египта — Осирион в Абидосе, нижний храм пирамиды Хафра и знаменитый большой Сфинкс — построены с применением того же измерительного комплекса. А возраст этих сооружений, как полагают некоторые исследователи, 10—15 тысяч лет. То есть наша русская система саженей имеет более чем почтенный возраст.

Осирион в Абидосе. Египет

Кстати говоря, мною проанализированы и известные мексиканские пирамиды, а также — Вавилонская башня. И все тот же расклад —древнерусская мерная система сажени. Все совпадает.

И НАШИ ПРЕДКИ ВОЗВОДИЛИ ПИРАМИДЫ В ДРЕВНЕМ ЕГИПТЕ?

— Из чего как бы следует: древнерусские сажени — общемировая данность?

— Общемировой «Всемер». И то, что мы до срока хранили золотую сажень, — не есть случайность. Это был наш крест, данный Свыше. Ничего случайного не происходит. Каждому народу «даются» какие-то знания для их сохранения и развития.
В 1947—1948 годах ныне мало кому известный ученый Эльвир Иванович Кучеренко, кандидат технических наук и в то же время специалист по древним измерительным инструментам и геральдике, выяснил во время экспедиции по Самарскому краю, что жители некоторых здешних районов «помнили», как их далекие предки строили знаменитые египетские пирамиды. Как вам сие нравится? Откуда они это взяли? Пусть это своего рода миф, но ведь он передается из поколения в поколение. О том же говорят, кстати, старожилы Полтавской, Брянской областей (Э.И.Кучеренко сам мне об этом рассказывал, и в широкой печати эти сведения появляются впервые).
А ведомо ли вам, как в тех же 40-х годах в Горьковской области замеряли вес стога сена? Сейчас все просто: загрузил машину и на весы. А как быть, когда у тебя лишь телега и лошадь? Так вот, мужик снимал вожжи и перебрасывал их поперек через стог. Потом опять перебросил, опять что-то прикинул, сложил что-то. И так, скажем, раз семь. А потом уверенно говорит: вес стога — полторы тонны. Его не надо было проверять. Все точно. Откуда он взял такой способ взвешивания? А способ-то — древнеегипетский!
Пойдем дальше. В 1927 году наша Академия наук расшифровала один из древнеегипетских папирусов. Оказалось, в нем был записан математический счет умножения. В это же время из Полтавской области возвращается экспедиция, проводившая там археологические раскопки. Один из ученых, когда был постояльцем у местного крестьянина, обратил внимание, как тот считает. А хозяин избы считал весьма странным образом. И только потом, после расшифровки папируса, выяснилось, что крестьянин считал прямо-таки «по папирусу»! Откуда полтавский землепашец мог знать древнеегипетский счет?
Вам хорошо известна загадка происхождения письменности. Древнейшей считается шумерская. Но кем, где и когда она зачиналась и развивалась, неизвестно [В середине XX века в балкано-карпатском регионе (в местах, связанных с формированием протославянского этноса) найдены еще не расшифрованные памятники письменности, которые на тысячи лет старше шумерских. — Ред.]. Шумеры владели развитой письменностью, и яснее ясного: она была изобретена много раньше. И нет ничего невероятного в допущении, что задолго до Шумера и Египта на Земле существовала высокоразвитая цивилизация. Вот, например, знаменитая карта турецкого адмирала Пири Рейса, на которой значительная часть Антарктиды достаточно подробно изображена безо всякого ледникового покрова. Дискуссии по сему вопросу не смолкают до сих пор. Но мало кто знает об открытии американского ученого Ч.Хэпгуда. Еще полвека назад, построив карту современного типа на основании системы проекций Пири Рейса, он обнаружил, что нулевой меридиан этой системы проекций — примерно 30 градусов восточной долготы — проходит… через Нижний Египет, через комплекс пирамид!

— Хорошо. Давайте, Анатолий Федорович, все же остановимся и хотя бы сами себе ответим: откуда все это? Вы намекаете на некие связи с какими-то доисторическими цивилизациями, пришельцами? Или имеете в виду Космический Разум?

— При чем тут пришельцы? Мне думается так: все неожиданные, необъяснимые открытия, все потаенные знания наших предков — в том числе удивительная система древнерусских саженей — все это имеет Божественное происхождение. Ведь от Бога пошло Слово — то есть Знания… И я не без оснований утверждаю: сам по себе человек не мог открыть столь совершенную гармонию, как золотые пропорции в системе древнерусских измерений.
Мы обладаем инструментом сказочных возможностей. С помощью русской матрицы нам под силу не только создавать какие угодно объекты в рамках золотых пропорций; появляется реальная возможность контролировать правильность протекания самых различных технологических процессов, связанных с материальным производством. То есть сами соотношения этих процессов станут внутренне красивыми, совершенными, поскольку будут подчиняться «золотому мерилу», сохраненному для нас зодчими Древней Руси…

Источник: http://svetlota.by.ru/nebschet.htm

Источник

А.Ф. Черняев ЗОЛОТО ДРЕВНЕЙ РУСИ. РУССКАЯ МАТРИЦА — ОСНОВА ЗОЛОТЫХ ПРОПОРЦИЙ

Еще статья на эту тему:
Древнерусский всемер при строительстве пирамид в Гизе

Доказательство существования строгой пропорциональной системы древнерусских саженей