alexxlabПрименение дробей
Этот урок будет интересным и познавательным. Мы научимся применять дроби для различных жизненных случаев.
Нахождение дроби от числа
Мы уже говорили, что дробь это часть от чего-либо. Эта часть может быть чем угодно. Например, от пиццы это половина пиццы:
Но применение дробей не заканчивается на одной пицце. Например, можно узнать сколько составляет от десяти сантиметров:
Как вы уже догадались от десяти сантиметров составляют пять сантиметров. Ведь это простейшая дробь, которая означает половину от чего-то. У нас было десять сантиметров. Мы разделили эти десять сантиметров пополам и получили пять сантиметров.
Попробуем узнать, сколько составляет от одного часа. Вспоминаем, что час это 60 минут. Нам нужно найти (половину) от 60 минут. Нетрудно догадаться, что половина от 60 минут это 30 минут. Значит от одного часа составляет 30 минут или полчаса.
Попробуем найти от одного центнера. Центнер это 100 кг. Требуется найти (половину) от 100 кг. Нетрудно догадаться, что половина от 100 кг это 50 кг. Значит от одного центнера составляют 50 кг.
Поскольку мы занимаемся математикой, значит в большинстве случаев будем иметь дело с числами. Например, найдём от числа 12.
Итак, нужно найти половину от числа 12. Нетрудно догадаться, что половиной от числа 12 является число 6. Значит числа 12 составляет число 6.
Чтобы легче было находить дробь от числа, можно пользоваться следующим правилом:
Чтобы найти дробь от числа, нужно это число разделить на знаменатель дроби, и полученный результат умножить на числитель дроби.
Попробуем проследить весь процесс работы этого правила. Для примера возьмём десять сантиметров:
Пусть требуется найти от этих десяти сантиметров. Читаем первую часть правила:
Чтобы найти дробь от числа, нужно это число разделить на знаменатель дроби
Итак, делим десять сантиметров на знаменатель дроби . Знаменатель этой дроби равен числу 2. Поэтому делим десять сантиметров на 2
10 см : 2 = 5 см
Читаем вторую часть правила:
и полученный результат умножить на числитель дроби
Итак, умножаем пять сантиметров на числитель дроби . Числитель дроби в данном случае единица. Поэтому умножаем пять сантиметров на единицу:
5 см × 1 = 5 см
Мы нашли от десяти сантиметров. Видим, что от десяти сантиметров составляют пять сантиметров:
Почему же после деления числа на знаменатель дроби приходиться умножать полученный результат на числитель дроби? Дело в том, что знаменатель дроби показывает на сколько частей что-либо разделено, а числитель показывает сколько частей было взято.
В нашем примере десять сантиметров были разделены на две части (пополам), и из этих частей была взята одна часть. Умножая одну часть на числитель дроби, мы тем самым указываем сколько частей мы берём от чего-то. То есть умножив пять сантиметров на числитель дроби , мы тем самым указали, что берем одну часть из двух.
Пример 2. Найти от 10 см.
Применим правило нахождения дроби от числа:
Чтобы найти дробь от числа, нужно это число разделить на знаменатель дроби, и полученный результат умножить на числитель дроби.
Сначала делим 10 сантиметров на знаменатель дроби
10 см : 5 = 2 см
Получили два сантиметра. Этот результат нужно умножить на числитель дроби
2 см × 2 = 4 см
Мы нашли от десяти сантиметров. Видим, что от десяти сантиметров составляют четыре сантиметра.
Весь процесс решения можно увидеть на следующем рисунке:
Сначала десять сантиметров были разделены на пять равных частей. Затем было взято две части из этих пяти частей:
Пример 3. Найти от числа 56.
Чтобы найти от числа 56, нужно это число разделить на знаменатель дроби , и полученный результат умножить на числитель дроби .
Итак, сначала делим число 56 на знаменатель дроби
56 : 8 = 7
Теперь умножаем полученное результат на числитель дроби
7 × 3 = 21
Получили ответ 21. Значит от числа 56 составляет 21.
Пример 4. Найти от одного часа.
Один час это 60 минут. Задание можно понимать, как нахождение от 60 минут.
Сначала разделим 60 минут на знаменатель дроби
60 мин : 4 = 15 мин
Теперь умножим полученные 15 минут на числитель дроби
15 мин × 2 = 30 мин
Получили в ответе 30 минут. Значит от одного часа составляют тридцать минут или полчаса.
Пример 5. Найти от одного метра.
Один метр это сто сантиметров. Сначала разделим 100 см на знаменатель дроби
100 см : 5 = 20 см
Теперь умножим полученные 20 см на числитель дроби
20 см × 4 = 80 см
Получили ответ 80 см. Значит от одного метра составляют 80 см.
Нахождение целого числа по дроби
Зная часть числа и сколько это составляет от целого числа, можно найти изначальное целое число. Это обратная задача к той, которую мы рассматривали в предыдущей теме. Там мы искали дробь от числа, деля это число на знаменатель дроби, и полученный результат умножая на числитель дроби.
А сейчас наоборот, зная дробь и сколько это составляет от числа, найти изначальное целое число.
Например, если длины линейки составляют шесть сантиметров и нам говорят найти длину всей линейки, то мы должны понимать, что от нас требуют найти изначальное целое число (длину всей линейки) по дроби . Давайте решим эту задачу.
Требуется найти длину всей линейки по дроби . Известно, что длины всей линейки составляют 6 см.
Мы уже знаем каким образом получились эти 6 см. Имелась какая-то длина, её разделили на пять частей, поскольку знаменатель дроби это число 5. Затем было взято две части от пяти частей, поскольку числитель дроби это число 2.
Чтобы узнать длину всей линейки, сначала нужно узнать длину одной части. Как это узнать? Попробуем догадаться, внимательно изучив следующий рисунок:
Если две части длины линейки составляют 6 см, то нетрудно догадаться, что одна часть составляет 3 см. А чтобы получить эти 3 см, надо 6 разделить на 2
6 см : 2 = 3 см
Итак, мы нашли длину одной части. Одна часть из пяти или длины линейки составляет 3 см. Если частей всего пять, то для нахождения длины линейки, нужно взять три сантиметра пять раз. Другими словами, умножить 3 см на число 5
3 см × 5 = 15
Мы нашли длину линейки. Она составляет 15 сантиметров. Это можно увидеть на следующем рисунке.
Видно, что пять частей из пяти или составляют пятнадцать сантиметров.
Чтобы легче было находить число по его дроби, можно пользоваться следующим правилом:
Чтобы найти число по его дроби, нужно известное число разделить на числитель дроби, и полученный результат умножить на знаменатель дроби.
Пример 2. Число 20 это от всего числа. Найдите это число.
Знаменатель дроби показывает, что число, которое мы должны найти, разделено на пять частей. Если этого числа составляет число 20, то для нахождения всего числа, сначала нужно найти (одну часть из пяти) от всего числа. Для этого 20 надо разделить на числитель дроби
20 : 4 = 5
Мы нашли от всего числа. Эта часть равна 5. Чтобы найти всё число, нужно полученный результат 5 умножить на знаменатель дроби
5 × 5 = 25
Мы нашли от всего числа. Другими словами, нашли всё число, которое от нас требовали найти. Это число 25.
Пример 3. Десять минут это времени приготовления каши. Найдите общее время приготовления каши.
Знаменатель дроби показывает, что общее время приготовления каши разделено на три части. Если времени приготовления каши составляет десять минут, то для нахождения общего времени приготовления, нужно сначала найти времени приготовления. Для этого 10 нужно разделить на числитель дроби
10 мин : 2 = 5 мин
Мы нашли времени приготовления каши. времени приготовления каши составляют пять минут. Для нахождения общего времени приготовления, нужно 5 минут умножить на знаменатель дроби
5 мин × 3 = 15 мин
Мы нашли времени приготовления каши, то есть нашли общее время приготовления. Оно составляет 15 минут.
Пример 4. массы мешка цемента составляет 30 кг. Найти общую массу мешка.
Знаменатель дроби показывает, что общая масса мешка разделена на четыре части. Если массы мешка составляет 30 кг то для того, чтобы найти общую массу мешка нужно сначала найти массы мешка. Для этого 30 надо разделить на числитель дроби .
30кг : 2 = 15кг
Мы нашли массы мешка. массы мешка составляет 15 кг. Теперь, чтобы найти общую массу мешка, надо 15кг умножить на знаменатель дроби
15кг × 4 = 60кг
Мы нашли массы мешка. Другими словами, нашли общую массу мешка. Общая масса мешка цемента составляет 60 кг.
Деление меньшего числа на большее
В жизни часто возникают ситуации, когда требуется разделить меньшее число на большее. Например, представим ситуацию. Имеется трое друзей:
И требуется поровну разделить между ними два яблока. Как это сделать? Друзей трое, а яблок всего два. Мы попали в ситуацию в которой требуется разделить меньшее число на большее (два яблока на троих).
Для таких случаев предусмотрено следующее правило:
При делении меньшего числа на большее получается дробь, в числителе которой делимое, а в знаменателе – делитель.
Давайте применим это правило. Оно говорит, что при делении меньшего числа на большее получается дробь, в числителе которой делимое, а в знаменателе делитель. Делимое у нас это два яблока. Записываем в числителе число 2:
А делитель у нас это трое друзей (вспоминаем, что делитель показывает на сколько частей надо разделить делимое). Записываем тройку в знаменателе нашей дроби:
Забавно, но дробь это ответ к нашей задаче. Каждому другу достанется яблока. Почему так произошло?
Чтобы разделить два яблока на троих, надо разрезать ножом каждое яблоко на три части и раскидать поровну эти куски между тремя друзьями:
Как видно на рисунке, каждое яблоко было разделено на три части и раскидано поровну на троих друзей. Каждому другу досталось яблока (два кусочка из трёх).
Какую часть одно число составляет от другого
Иногда возникает необходимость узнать какую часть первое число составляет от второго. Для таких случаев предусмотрено следующее правило:
Чтобы узнать какую часть первое число составляет от второго, надо первое число разделить на второе.
Например, яблоко разделили на пять одинаковых долек. Какую часть яблока составляют две дольки?
Чтобы ответить на этот вопрос, надо первое число разделить на второе. Первое число это 2, второе — 5. Получается дробь .
Значит две дольки из пяти долек составляют две пятых. Это можно увидеть на следующем рисунке:
Итак, две дольки яблока из пяти составляют две пятых.
Возникает вопрос, а как узнать какое число первое, а какое второе? Для этого нужно посмотреть на вопрос, который поставлен в задаче. То число, которое указано в вопросе задачи, оно и будет первым числом. Например, в предыдущей задаче вопрос был поставлен так:
«Какую часть яблока составляют две такие дольки?»
Если внимательно присмотреться к вопросу, то можно обнаружить, что в нём указано число 2. Оно и стало первым числом.
Иногда в вопросе мелькает сразу два числа. Например: какую часть составляет число 2 от числа 10?
В этом случае первым числом будет то, которое в вопросе расположено раньше. В данном случае первое число это 2, а второе 10. Делим 2 на 10, получаем дробь . Значит число 2 от числа 10 составляет (две десятых).
Дробь означает, что число 10 разделено на десять частей, и от этих десяти частей взято две части.
Также, эту дробь можно сократить на 2. После сокращения дроби на 2 получаем дробь .
Дробь тоже может послужить ответом к задаче. Она будет означать, что число 10 разделено на пять частей, и от этих пяти частей взята одна часть.
Таким образом, число 2 составляет (одну пятую) от числа 10.
Пример 3. Какую часть составляет число 5 от числа 15?
Делим первое число на второе. Первое число 5, а второе 15. Делим 5 на 15, получаем дробь . Эту дробь можно сократить на 5
Получили аккуратную дробь . Значит ответ будет выглядеть следующим образом:
Число 5 составляет (одну третью) от числа 15.
Это можно даже проверить. Для этого нужно найти от числа 15. Если мы всё сделали правильно, то должны получить число 5.
Итак, найдём от числа 15. Как находить дробь от числа мы уже знаем
15 : 3 = 5
5 × 1 = 5
Получили ответ 5. Значит задача была решена правильно.
Пример 4. Какую часть 3 см составляют от 12 см?
Делим первое число на второе. Первое число это 3, а второе 12. Получаем дробь . Эту дробь можно сократить на 3
Получили ответ . Значит 3 см составляют (одну четвёртую) от 12 см.
Проверим правильно ли мы решили эту задачу. Для этого найдём от 12 см. Если мы всё сделали правильно, то должны получить 3 см.
Делим 12 на знаменатель дроби
12 см : 4 = 3 см
Умножаем полученные 3 см на числитель дроби
3 см × 1 = 3 см
Получили ответ 3 см. Значит задача была решена правильно.
Задания для самостоятельного решения
Задание 1. Найдите от числа 30. Задание 2. Найдите от числа 30. Задание 3. Найдите от числа 30. Задание 4. Найдите от числа 48. Задание 5. Найдите от числа 48. Задание 6. Найдите от 120 см.120 см : 3 = 40 см
40 см × 2 = 80 см
150 см : 3 = 50 см
50 см × 2 = 100 см
150 : 5 = 30
30 × 8 = 240
4 км : 2 = 2 км
2 км × 3 = 6 км
100 см : 5 = 20 см
20 см × 8 = 160 см
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
Навигация по записям
Дробные выражения. Видеоурок. Математика 6 Класс
Что же такое дробь? Например, дробь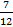 
– это деление числа 7 на число 12, записанное с помощью дробной черты.
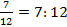
Частное двух чисел или выражений, в котором знак деления обозначен чертой, называют дробным выражением.
Примеры дробных выражений:
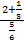
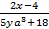
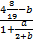
Дробь 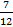также является дробным выражением.
У дробного выражения существуют эквивалентные, равные ему, выражения. Выбрать из всех эквивалентных выражений самое простое – значит упростить дробное выражение.
Пример
Упростить дробное выражение:
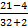
Решение
Выполним вычитание в числители и сложение в знаменателе:
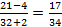
Разделим числитель и знаменатель на 17:
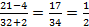
Ответ: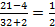 
.
Упростите дробное выражение:
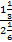
Решение
В числителе и знаменателе – смешанные дроби. Чтобы разделить одну смешанную дробь на другую, нужно обе записать как неправильные.
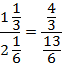
Получившееся дробное выражение эквивалентно произведению дробных выражений:
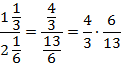
Сократим знаменатель первой дроби и числитель второй дроби на 3:
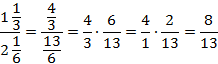
Ответ: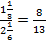 
.
Сложите дробные выражения:
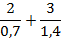
Решение
1 способ
Приведем эти дробные выражения к одному знаменателю, для этого умножим числитель и знаменатель первой дроби на 2:
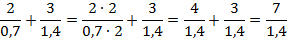
Чтобы избавиться от десятичной дроби в знаменателе, умножим числитель и знаменатель на 10:
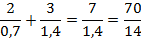
Сократим числитель и знаменатель на 7:
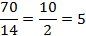
2 способ
Можно сразу избавиться от десятичных дробей в знаменателях, для этого умножим числитель и знаменатель каждой дроби на 10:
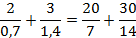
Далее приводим два дробных выражения к общему знаменателю:
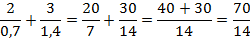
Сократим числитель и знаменатель на 7:
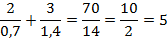
Ответ: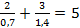 
.
Упростите дробное выражение:
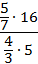
Решение
Преобразуем числитель и знаменатель в обыкновенные дроби:
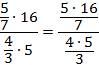
Запишем получившееся выражение с помощью знака деления:
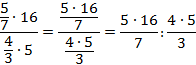
Чтобы разделить на дробь, нужно умножить на перевернутую дробь:
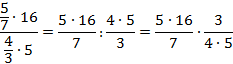
Числитель первой дроби и знаменатель второй можно сократить на 5 и на 4:
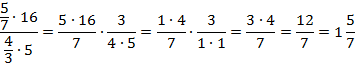
Ответ: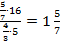 
.
Упростите дробное выражение:
1. 
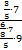
Решение
Преобразуем числитель и знаменатель в обыкновенные дроби:
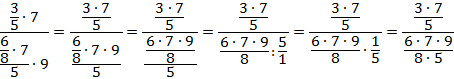
Запишем это дробное выражение с помощью знака деления, а далее заменим знак деления на знак умножения и перевернем вторую дробь:
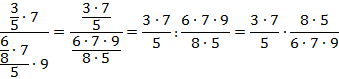
Сократим числитель первой дроби и знаменатель второй на 3 и 7, а числитель второй дроби и знаменатель первой – на 5:
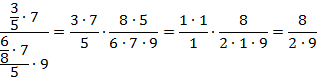
Сократим числитель и знаменатель на 2:
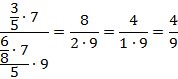
2) 
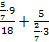
Решение
Преобразуем числитель первого дробного выражения и знаменатель второго:
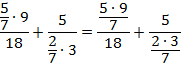
Распишем данные дробные выражения с помощью знака деления:
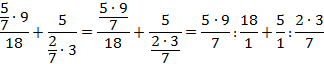
Заменим знаки деления на знаки умножения и перевернем соответствующие дроби:
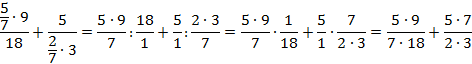
Первое дробное выражение сократим на 9:
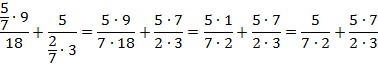
Приведем дробные выражения к общему знаменателю, для этого числитель и знаменатель первого выражения умножим на 3, а числитель и знаменатель второго выражения умножим на 7:
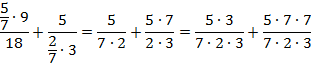
Вычислим числители обеих дробей и сложим эти дроби:
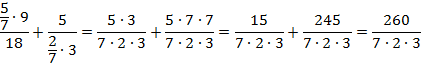
Сократим полученную дробь на 2:
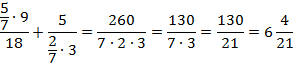
Ответ: 1.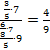 
; 2.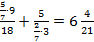 
.
Преобразование «многоэтажных» дробей
Существует очень простой алгоритм, который позволяет за одно действие разобрать «многоэтажную» дробь и получить обычную «двухэтажную».
Необходимо после знака равно начертить дробную черту и для каждого элемента из «многоэтажной» дроби найти его место в новой дроби. Для этого нужно рассмотреть каждое число в исходной дроби.
Если число находилось в исходной дроби нечетное число раз в знаменателе, то в новой дроби оно окажется в знаменателе; если число находилось в исходной дроби четное число раз в знаменателе или не находилось в знаменателе вообще, то в новой дроби оно окажется в числителе.
Рассмотрим примеры.
Упростите дробные выражения.
1. 
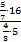
Рассмотрим каждое число данного дробного выражения:
Число 5 (в данном выражении две пятерки, их рассматриваем отдельно) находится в числителе дроби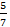 
и в числителе всего исходного дробного выражения. То есть не находится в знаменателе, следовательно, в новой дроби это число окажется в числителе;
число 7 находится в знаменателе дроби 
и в числителе всего исходного дробного выражения. То есть находится в знаменателе нечетное число раз, следовательно, в новой дроби это число окажется в знаменателе;
число 16 находится в числителе всего исходного дробного выражения. То есть не находится в знаменателе, следовательно, в новой дроби это число окажется в числителе;
число 4 находится в числителе дроби 
и в знаменателе всего исходного дробного выражения. То есть находится в знаменателе нечетное число раз, следовательно, в новой дроби это число окажется в знаменателе;
число 3 находится в знаменателе дроби и в знаменателе всего исходного дробного выражения. То есть находится в знаменателе четное число раз, следовательно, в новой дроби это число окажется в числителе;
число 5 находится в знаменателе всего дробного выражения. То есть находится в знаменателе нечетное число раз, следовательно, в новой дроби это число окажется в знаменателе.
Запишем полученное дробное выражение:
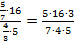
Сократим числитель и знаменатель на 5 и на 4:
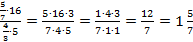
2.
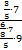
Рассмотрим каждое число данного дробного выражения:
Число 3 не находится в знаменателе, следовательно, в новой дроби это число окажется в числителе;
число 5 находится в знаменателе дроби 
, то есть нечетное количество раз, следовательно, в новой дроби это число окажется в знаменателе;
число 7 не находится в знаменателе, следовательно, в новой дроби это число окажется в числителе;
число 6 находится в знаменателе всего дробного выражения, то есть нечетное количество раз, следовательно, в новой дроби это число окажется в знаменателе;
число 8 находится в знаменателе дроби 
и в знаменателе всего дробного выражения, то есть четное количество раз, следовательно, в новой дроби это число окажется в числителе;
число 7 находится в знаменателе всего дробного выражения, то есть нечетное количество раз, следовательно, в новой дроби это число окажется в знаменателе;
число 5 находится в знаменателе всего дробного выражения и в знаменателе выражения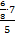 
, то есть четное количество раз, следовательно, в новой дроби это число окажется в числителе;
число 9 находится в знаменателе всего дробного выражения, то есть нечетное количество раз, следовательно, в новой дроби это число окажется в знаменателе.
Запишем полученное дробное выражение:
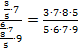
Сократим числитель и знаменатель на 5, 7, 2 и 3:
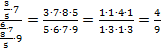
3.
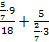
Рассмотрим числа в каждом дробном выражении:
а) выражение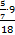 
Число 5 не находится в знаменателе, следовательно, в новой дроби это число окажется в числителе;
число 7 находится в знаменателе дроби , то есть нечетное количество раз, следовательно, в новой дроби это число окажется в знаменателе;
число 9 не находится в знаменателе, следовательно, в новой дроби это число окажется в числителе;
число 18 находится в знаменателе всего дробного выражения, то есть нечетное количество раз, следовательно, в новой дроби это число окажется в знаменателе.
б) выражение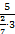 
Число 5 не находится в знаменателе, следовательно, в новой дроби это число окажется в числителе;
число 2 находится в знаменателе всего дробного выражения, то есть нечетное количество раз, следовательно, в новой дроби это число окажется в знаменателе;
число 7 находится в знаменателе дроби 
и в знаменателе всего дробного выражения, то есть четное количество раз, следовательно, в новой дроби это число окажется в числителе;
число 3 находится в знаменателе всего дробного выражения, то есть нечетное количество раз, следовательно, в новой дроби это число окажется в знаменателе.
Запишем полученные дробные выражения:
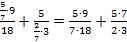
Сократим числитель и знаменатель первого выражения на 9:
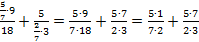
Приведем дробные выражения к общему знаменателю, для этого числитель и знаменатель первого выражения умножим на 3, а числитель и знаменатель второго выражения умножим на 7:
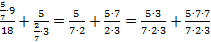
Вычислим числители обеих дробей и сложим эти дроби:
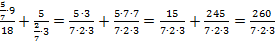
Сократим полученную дробь на 2:
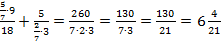
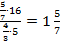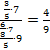Ответ: 1. ; 2. ; 3. .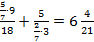
Чтобы найти значение выражения с переменными, необходимо подставить в это выражение значения этих переменных. Но предварительно имеет смысл упростить выражение, если это возможно.
Найти значение выражения.
1. 
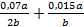, при 
; 
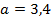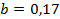
Решение
Упростим данное выражение. Приведем слагаемые к общему знаменателю, для этого умножим числитель и знаменатель второй дроби на 2:
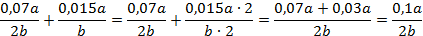
Подставим в полученное выражение значение переменных:
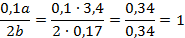
2. 
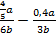, при 
; 
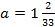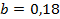
Решение
Упростим данное выражение. Приведем слагаемые к общему знаменателю, для этого умножим числитель и знаменатель второй дроби на 2:
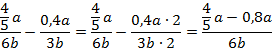
Так как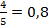 
, то:
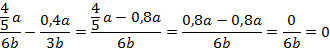
Мы получили ответ, даже не подставив значения переменных.
Ответ: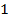 
. 1; 2. 0.
Список литературы
1. Виленкин Н.Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И. Математика 6. – М.: Мнемозина, 2012.
2. Мерзляк А.Г., Полонский В.В., Якир М.С. Математика 6 класс. – Гимназия. 2006.
3. Депман И.Я., Виленкин Н.Я. За страницами учебника ма
Изготовление дроби
Сегодня такое увлечение, как охота является довольно затратным хобби и, безусловно, не все охотники могут позволить себе охотиться так часто как бы им этого хотелось. Особенно это касается новичков, у которых процент попадания не так уж и велик. Именно поэтому многие охотники отдают предпочтение самостоятельному производству дроби. И это верный путь, так как с помощью него можно не только сэкономить на покупке зарядов, но и пристрелявшись, оптимально подобрать его для своего ружья.
Сегодня мы расскажем о давно известном и наиболее практичном способе самостоятельного изготовления дроби в домашних условиях.
Наиболее распространенный среди охотников метод – это изготовление дроби подручными средствами, а именно с помощью сковородки, свинца, магнита, тазика и водопроводной воды. Благодаря этим компонентам у вас получится отличная дробь пятого номера. В принципе, какой номер выбрать каждый охотник решит для себя сам, так как его можно регулировать, меняя диаметр отверстия и температуру плавки, как это происходит, вы поймете позже.
Подготовка и процесс изготовления
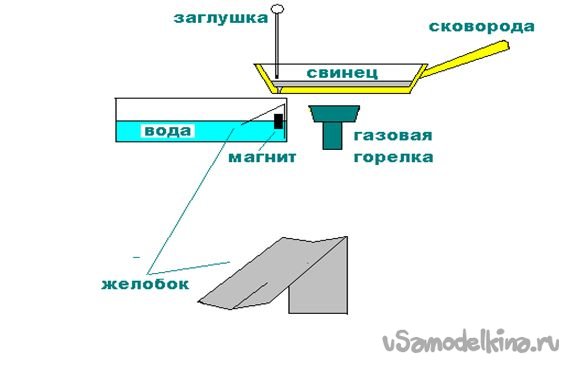
Для этого нам понадобится старая ненужная сковородка, на краю дна которой, мы просверливаем отверстие диаметром 0,7 миллиметра, закупорив ее заглушкой. В качестве временной заглушки можно использовать гвоздь либо стальную проволоку подходящего диаметра. Ставим сковороду на газ и закидываем в нее свинец, примерно 2–3 килограмма. Далее, нужен металлический тазик, который наполняем водой (лучше использовать патоку), желательно до краев, и располагаем его непосредственно под сковородой. Идеальным расстоянием между тазиком и сковородой будет примерно от одного сантиметра до двух. Далее, крепим желобок к краю тазика при помощи магнита. Предварительно будет целесообразно обтянуть желобок фланелью либо шелком и хорошенько намочить. Здесь важно знать, что при изготовлении крупной дроби желобок следует убрать, а мелкой, естественно, наоборот.
Перед проведением вышеописанной работы обратите внимание на величину дроби, которую вы хотите получить в итоге. Здесь важно учитывать не только диаметр отверстия, но также и температуру плавления, так как при быстрой плавке, свинец вытекает быстрее, и дробь, соответственно, получается крупная. Если вы все сделали по инструкции, но шарики все равно получаются неидеальные, например, овальной формы, то следует немного увеличить высоту сковородки от желобка, либо спустить сам желобок, регулируя его с помощью магнита.
Источник
Доставка новых самоделок на почтуПолучайте на почту подборку новых самоделок. Никакого спама, только полезные идеи!
*Заполняя форму вы соглашаетесь на обработку персональных данных
Становитесь автором сайта, публикуйте собственные статьи, описания самоделок с оплатой за текст. Подробнее здесь.определения, обозначения, примеры, действия с дробями, числитель и знаменатель
Рассмотрение данной темы мы начнем с изучения понятия доли в целом, которое даст нам более полное понимание смысла обыкновенной дроби. Дадим основные термины и их определение, изучим тему в геометрическом толковании, т.е. на координатной прямой, а также определим список основных действий с дробями.
Доли целого
Представим некий предмет, состоящий из нескольких, совершенно равных частей. Например, это может быть апельсин, состоящий из нескольких одинаковых долек.
Определение 1Доля целого или доля – это каждая из равных частей, составляющих целый предмет.
Очевидно, что доли могут быть разные. Чтобы наглядно пояснить это утверждение, представим два яблока, одно из которых разрезано на две равные части, а второе – на четыре. Ясно, что размеры получившихся долей у разных яблок будут различаться.
Доли имеют свои названия, которые зависят от количества долей, составляющих целый предмет. Если предмет имеет две доли, то каждая из них будет определяться как одна вторая доля этого предмета; когда предмет состоит из трех долей, то каждая из них – одна третья и так далее.
Определение 2Половина – одна вторая доля предмета.
Треть – одна третья доля предмета.
Четверть – одна четвертая доля предмета.
Чтобы сократить запись, ввели следующие обозначения долей: половина — 12 или 1/2; треть — 13 или 1/3; одна четвертая доля — 14 или 1/4 и так далее. Записи с горизонтальной чертой используются чаще.
Понятие доли естественно расширяется с предметов на величины. Так, можно использовать для измерения небольших предметов доли метра (треть или одна сотая), как одной из единиц измерения длины. Аналогичным образом можно применить доли других величин.
Обыкновенные дроби, определение и примеры
Обыкновенные дробиприменяются для описания количества долей. Рассмотрим простой пример, который приблизит нас к определению обыкновенной дроби.
Представим апельсин, состоящий из 12 долек. Каждая доля тогда будет – одна двенадцатая или
Дополнительные сведения о дробях
В этом уроке мы коснёмся тех моментов, о которых не упоминали при изучении дробей, посчитав что на первых порах они создают трудности для обучения.
Правильные и неправильные дроби
В самом начале своего пути при изучении дробей мы узнали, что правильная дробь — это та дробь, у которой числитель меньше знаменателя.
В школьной литературе можно встретить другое определение правильной дроби. Выглядит оно следующим образом:
Правильная дробь всегда меньше единицы.
Как понять данное определение? Дробь сама по себе указывает на то, что какой-либо объект разделен на несколько частей. И это всегда один единственный объект. Под единицей именно это и подразумевается.
Например, пусть у нас имеется одна пицца:
В данном случае она и является единицей.
Если мы отрежем от этой пиццы половину, то есть (одну вторую пиццы), то наш кусок будет меньше, чем вся целая пицца:
В этом и заключается суть фразы «правильная дробь всегда меньше единицы».
Наша половинка пиццы является дробью и она меньше одной целой пиццы, то есть меньше единицы:
Это выражение можно доказать. Если мы вычислим дробь , то получим десятичную дробь 0,5. А это рациональное число меньше единицы:
На координатной прямой можно увидеть, как располагаются эти числа:
Видно, что рациональное число 0,5 располагается левее, чем 1. А мы помним, что чем левее число располагается на координатной прямой, тем оно меньше.
С неправильными дробями всё было наоборот. Неправильной дробью мы назвали ту дробь, у которой числитель больше знаменателя.
Но в школьной литературе можно встретить другое определение неправильной дроби. Выглядит оно следующим образом:
Неправильная дробь всегда больше единицы или равна ей.
Например, рассмотрим неправильную дробь . Выделим в этой дроби целую часть, получим . Изобразим эту смешанную дробь в виде одной целой пиццы и ещё половинки пиццы:
Вместе одна целая пицца и ещё половина пиццы больше, чем просто одна целая пицца
В этом и заключается суть фразы «неправильная дробь всегда больше единицы».
Одна целая пицца и ещё половина пиццы описывается смешанной дробью и эта смешанная дробь больше единицы:
Переведём смешанную дробь обратно в неправильную дробь, чтобы не противоречить правилу. Ведь речь в данном случае идёт о неправильных дробях:
что схематически будет выглядеть так:
Выражение можно доказать. Если мы вычислим дробь , то получим десятичную дробь 1,5. А это рациональное число больше единицы:
На координатной прямой можно увидеть, как располагаются эти числа:
Видно, что рациональное число 1,5 располагается правее, чем 1. А мы помним, что чем правее число располагается на координатной прямой, тем оно больше.
Неправильной также называется дробь равная единице. Речь в данном случае идет о тех дробях, у которых числитель и знаменатель равны.
Рассмотрим дробь . Изобразим её в виде двух одинаковых кусочков пиццы:
Фактически речь идёт не о дроби, а об одной целой пицце:
В этом и заключается суть фразы «неправильная дробь может равняться единице».
Любое целое число отличное от нуля (не равное нулю) можно представить в виде неправильной дроби со знаменателем 1. Например, числа 3, 5, 9, 12 можно представить в виде неправильных дробей со знаменателем 1
Представление объекта в виде единицы позволяет проще решать задачи. Рассмотрим примеры.
Пример 1. Куплен один шоколадный батончик. От него отрезали треть. Сколько батончика осталось?
Осталось две трети батончика. Сам батончик можно описать цифрой 1, далее из этой единицы вычесть треть:
Не приводя на бумаге никаких вычислений, можно ответить на вопрос подобной задачи. Сказано «отрезали треть» — значит сразу нужно обратить внимание на то, что знаменатель равен 3.
Если отрезали одну часть из трёх, то сколько частей должно остаться? Верно, две части. Поэтому и ответ «две части из трёх» или «две трети».
Пример 2. Куплен один пирог. От него отрезали две шестых. Сколько пирога осталось?
Осталось четыре шестых пирога. Сам пирог можно описать цифрой 1, далее из этой единицы вычесть две шестых:
Приведение дробей к общему знаменателю
Чтобы привести дроби к общему знаменателю, мы находили НОК (наименьшее общее кратное) знаменателей этих дробей. Затем делили найденный НОК на знаменатель первой дроби и получали дополнительный множитель для первой дроби.
То же самое мы делали и для второй дроби — делили НОК на знаменатель второй дроби и получали дополнительный множитель для второй дроби.
Затем дроби умножались на свои дополнительные множители. В результате они обращались в дроби, у которых одинаковые знаменатели. К примеру, выражение вычисляется следующим образом:
Но есть и другой способ приведения дробей к общему знаменателю. Этим способом часто пользуются школьники и ленивые студенты. Суть этого способа заключается в том, что роль дополнительных множителей берут на себя знаменатели обеих дробей, причем происходит это «крест-накрест» — знаменатель первой дроби становится дополнительным множителем второй дроби, а знаменатель второй дроби становится дополнительным множителем первой дроби.
Вычислим предыдущее выражение этим способом. Знаменатель первой дроби 2 становится дополнительным множителем второй дроби, а знаменатель второй дроби 6 становится дополнительным множителем первой дроби:
Далее числитель и знаменатель каждой дроби умножаем на свой дополнительный множитель и вычисляем:
Преимущество данного способа в том, что не нужно находить НОК знаменателей обеих дробей. В процессе вычисления всё выравнивается само. Единственный недостаток заключается в том, что выражение становится более длинным и корявым.
Сравните выражения, которые мы вычислили сначала первым способом, а затем вторым:
Выражение, вычисленное первым способом, намного аккуратнее и короче, нежели второе.
Вторым способом мы будем пользоваться при изучении алгебры. В алгебре работать с буквенными выражениями приходиться чаще, чем с числовыми.
К примеру, если перед нами будет стоять задача привести буквенное выражение к общему знаменателю, то у нас не будет другого выхода, кроме как воспользоваться методом «крест-накрест», то есть использовать второй способ, который мы сейчас рассмотрели:
Нахождение дроби от числа
Чтобы найти дробь от числа, мы делим это число на знаменатель искомой дроби и полученный результат умножаем на числитель искомой дроби.
Например, чтобы найти от 10 сантиметров, нужно 10 разделить на 5, и полученный результат умножить на 2
10 : 5 = 2
2 × 2 = 4
Получили ответ 4. Значит от десяти сантиметров составляют 4 сантиметра. Схематически это выглядит примерно так:
Но есть и второй вариант решения. Для нахождения от десяти сантиметров, достаточно умножить 10 на . Тогда мы получим тот же результат, как и в прошлый раз, но получим мы его в одно действие:
Поэтому можно взять на заметку следующее правило нахождения дроби от числа:
Чтобы найти дробь от числа, нужно это число умножить на искомую дробь.
Пример 2. Найти от двух часов.
Два часа это 120 минут. Чтобы найти от 120 минут, нужно 120 умножить на дробь
Значит от двух часов составляют 80 минут.
Нахождение числа по дроби
Чтобы найти всё число по его дроби, мы делили это число на числитель имеющейся дроби и полученный результат умножали на знаменатель имеющейся дроби.
Например, зная что рулетки составляет 12 см, мы можем найти длину всей рулетки. Для этого 12 нужно разделить на 2, и полученный результат умножить на 3
12 : 2 = 6
6 × 3 = 18
Получили 18. Значит длина всей рулетки равна 18 см.
Но есть и второй вариант решения. Для нахождения длины всей рулетки, достаточно 12 разделить на дробь . Тогда мы получим тот же результат, как и в прошлый раз, но получим мы его в одно действие:
Поэтому можно взять на заметку следующее правило нахождения числа по дроби:
Чтобы найти число по дроби, нужно это число разделить на данную дробь.
Пример 2. всего пути составляет 6 км. Найти длину всего пути.
Чтобы найти длину всего пути, достаточно 6 разделить на дробь
Получили ответ 15. Значит длина всего пути составляет 15 километров.
Десятичная точка в дробях
Запятую в десятичной дроби, которая отделяет целую часть от дробной, по-другому называют десятичной точкой.
Дело в том, что в некоторых источниках целая часть от дробной отделяется именно точкой, а не запятой. Например:
2.5 (две целых пять десятых)
15.65 (пятнадцать целых шестьдесят пять сотых)
Точка часто используется для записи десятичных дробей на компьютере — в программировании и при работе в математических пакетах. В остальных случаях: на письме и при подготовке документов, в десятичных дробях чаще используется запятая, а не точка.
Мы используем в десятичных дробях запятую, а не точку, поэтому разумнее называть эту запятую десятичной запятой.
Но десятичную запятую большинство людей тоже называют десятичной точкой. Что в принципе не является ошибкой, потому как речь всё равно идёт о разделителе, котором отделяет целую часть от дробной.
Давайте и мы будем называть свою запятую в десятичных дробях десятичной точкой. Это словосочетание проговаривается легче и приятнее на слух.
Десятичная точка используется для увеличения или уменьшения дроби в 10, 100, 1000 и более раз. При увеличении десятичной дроби, десятичная точка передвигается вправо, а при уменьшении — влево. Чтобы быстро запомнить это, можно воспользоваться фразами «чем правее, тем больше» и «чем левее, тем меньше».
Пример 1. Увеличить десятичную дробь 6,3 в десять раз.
Чтобы увеличить десятичную дробь 6,3 в десять раз, достаточно передвинуть десятичную точку вправо на одну цифру, получим 63.
Пример 2. Уменьшить десятичную дробь 6,3 в десять раз.
Для уменьшения дроби 6,3 в десять раз достаточно передвинуть десятичную точку влево на одну цифру, получим 0,63
На вопрос «как узнать на сколько цифр передвигать десятичную точку?», нужно смотреть во сколько увеличивается (или уменьшается) десятичная дробь. Если дробь нужно увеличить (или уменьшить) в десять раз, то десятичная точка сдвигается на одну цифру.
Если дробь нужно увеличить (или уменьшить) в сто раз, то десятичная точка сдвигается на две цифры.
Если дробь нужно увеличить (или уменьшить) в тысячу раз, то десятичная точка сдвигается на три цифры. В общем, всё зависит от количества нулей во множителе.
Например, увеличить дробь в десять раз означает умножить её на 10. Мы помним, что для того чтобы умножить десятичную дробь на 10, нужно в этой дроби передвинуть запятую вправо на одну цифру (поскольку в числе 10 один ноль). Теперь можно не заучивать подобные правила. Такое умножение можно легко выполнить, передвинув десятичную точку.
Пример 3. Увеличить десятичную дробь 6,3 в тысячу раз.
Чтобы увеличить десятичную дробь 6,3 в тысячу раз, достаточно передвинуть десятичную точку вправо на три цифры, получим 6300. Если после запятой не хватает цифр, то вместо недостающих цифр записывают нули, что мы и сделали.
Пример 4. Уменьшить десятичную дробь 12,5 в сто раз.
Для уменьшения дроби 12,5 в сто раз, достаточно передвинуть десятичную точку влево на две цифры, получим 0,125
Десятичную точку можно использовать не только в десятичных дробях. Её можно использовать для увеличения (уменьшения) и других чисел в 10, 100 или в 1000 раз.
Возьмём к примеру целое число 325 и поставим в конце точку, получим 325 с точкой. Воспользуемся в этот раз точкой, так как её легче изобразить на рисунке:
Попробуем уменьшить это число в десять раз. Для этого достаточно будет передвинуть точку влево на одну цифру, получим 32.5
Попробуем увеличить число 123 в тысячу раз. Для этого достаточно передвинуть десятичную точку на три цифры вправо, получим 123000.
Попробуем уменьшить число 123 в тысячу раз. Для этого достаточно передвинуть десятичную точку на три цифры влево, получим 0,123
Попробуем уменьшить число 65 в тысячу раз. Для этого достаточно передвинуть десятичную точку на три цифры влево, получим 0,065
Попробуем увеличить число 65 в сто раз. Для этого достаточно передвинуть десятичную точку на две цифры вправо, получим 6500.
Составные выражения
Встречаются задачи, в которых требуется вычислить выражение составленное из нескольких дробей. Например,
Такое выражение вычисляется согласно порядку действий. В данном случае вычисление будет выполнено последовательно слева направо:
Если из пиццы вычесть пиццы, затем прибавить пиццы, затем вычесть пиццы, то останется пиццы
Если вам тяжело понять данный пример, попробуйте самостоятельно решить его на бумаге, делая соответствующие рисунки к каждой дроби.
Пример 2. Найти значение выражения
В данном примере сначала необходимо выполнить умножение затем сложение и вычитание
Если пиццы увеличить в два раза, то получится одна целая пицца
Затем если к пиццы прибавить эту целую пиццу, а затем из полученного результата вычесть пиццы, то получится пиццы
Пример 3. Найти значение выражения
Сначала желательно вычислить выражения, находящиеся в числителях обеих дробей, а именно выражения 2−1 и 1+1,
Дальнейшее вычисление не составляет особого труда плюс равно
Конечно, можно было записать в одном числителе выражения, находящиеся в числителях обеих дробях. От этого ответ не изменился бы:
Но в некоторых случаях возможны подвохи, особенно если из одной дроби вычитается другая. Следующий пример демонстрирует это.
Пример 4. Найти значение выражения
Вычислим выражения, находящиеся в числителях обеих дробей, а именно выражения 2+1 и 2−1
Ну и нетрудно догадаться, что равно или (при условии, что дробь будет сокращена на 2)
Все логично. Если из пиццы вычесть пиццы, то получится пиццы.
Теперь попробуем решить данный пример, записав в одном числителе оба выражения, находящиеся в числителях обеих дробей:
Получается совсем другой ответ. Этот ответ не является правильным. Давайте посмотрим, что представляет собой выражение .
Для начала запишем его следующим образом:
Теперь попробуем проследить весь процесс вычисления этого выражения. Предположим, что имелось пиццы
К ней добавили еще пиццы
Затем из получившейся пиццы вычитается
Затем из получавшейся пиццы вычитают еще пиццы
Получился 0, то есть пицца исчезла. Но мы знаем, что должно было остаться пиццы. Поэтому при вычислении дробных выражений следует быть внимательным, особенно при вычитании выражений, содержащих в числителе другие выражения.
Если хочется сэкономить время и записать в числителе оба выражения, находящиеся в числителях обеих дробей, то второй числитель нужно взять в скобки. Это спасёт от ошибки:
Пример 5. Найти выражения
Вычислим выражения, находящиеся в числителях обеих дробей:
Приведем полученные дроби к общему знаменателю и как обычно вычислим полученное выражение:
Если из вычесть пиццы, то получится пиццы
Пример 6. Найти значение выражения
В первую очередь необходимо выполнить умножение:
Далее выполняется сложение:
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже