Обыкновенные дроби — Определение, Примеры, Действия, Доли, Числитель и Знаменатель

Поможем понять и полюбить математику

Начать учиться

301.8K

С 5 класса редкий урок математики проходит без дробей. Тема непростая и объемная, поэтому лучше начать разбираться сейчас, чтобы дальше было проще решать задачки. В этой статье расскажем про обыкновенные дроби.

Доля целого

Доля это каждая из равных частей, на которые поделено целое.

Для примера возьмем два мандарина. Когда мы их почистим, то получим в каждом мандарине разное количество долек или долей. В одном может быть 6, а в другом — целых 9. Размеры долей у каждого мандарина тоже разные.

У каждой доли есть свое название: оно зависит от количества долей в конкретном предмете. Если в мандарите шесть долей — каждая из них будет определяться, как одна шестая от целого.

• Половина — одна вторая доля предмета или 1/2.
• Треть — одна третья доля предмета или 1/3.
• Четверть — одна четвертая доля предмета или 1/4.

Понятие доли можно применить не только к предметам, но и величинам. Так, например, картина занимает четверть стены — при этом ее ширина треть метра.

Узнай, какие профессии будущего тебе подойдут

Пройди тест — и мы покажем, кем ты можешь стать, а ещё пришлём подробный гайд, как реализовать себя уже сейчас

Как устроена обыкновенная дробь

Обыкновенная дробь — это запись вида m/n, где m и n любые натуральные числа.

Такие дроби записываются с помощью двух натуральных чисел и горизонтальной черты, которая называется чертой дроби. Иногда ставится не горизонтальная черта, а косая.

Числитель обыкновенной дроби m/n — это натуральное число m, которое стоит над чертой.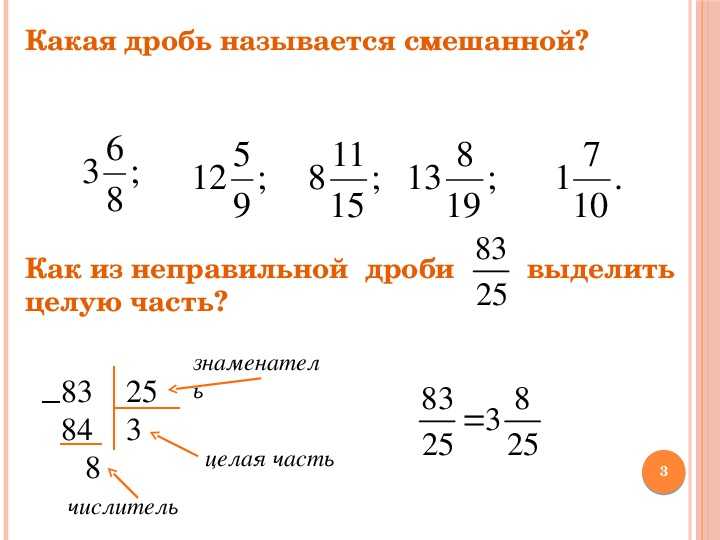 Числитель это делимое — то, что мы делим.

Знаменатель обыкновенной дроби m/n — натуральное число n, которое стоит под чертой. Знаменатель это делитель — то, на сколько делим.

Черта между числителем и знаменателем — символ деления.

Равные обыкновенные дроби — обыкновенные дроби a/b и c/d, для которых справедливо равенство: a * d = b * c. Пример равных дробей: 1/2 и 2/4, так как 1 * 4 = 2 * 2.

Неравные обыкновенные дроби — обыкновенные дроби a/b и c/d, для которых равенство: a * d = b * c не является верным.

Как устроена десятичная дробь

В десятичной дроби знаменатель всегда равен 10, 100, 1000, 10000 и т.д. Выходит, что десятичная дробь — это то, что получается, если разделить числитель на знаменатель. Десятичную дробь записывают в строчку через запятую, чтобы отделить целую часть от дробной. Вот так:

• 0,3
• 4,23
• 9,939

Конечная десятичная дробь — это дробь, в которой количество цифр после запятой точно определено.

Бесконечная десятичная дробь — это когда после запятой количество цифр бесконечно. Для удобства математики договорились округлять эти цифры до 1-3 после запятой.

Свойства дробей

Основное свойство дроби: если числитель и знаменатель дроби умножить или разделить на одно и то же отличное от нуля число, то получится дробь, равная данной. Формула выглядит так:

где a, b, k — натуральные числа.

Основные свойства Дробь не имеет значения, если знаменатель равен нулю. Дробь равна нулю, если числитель равен нулю, а знаменатель — нет. Две дроби a/b и c/d называются равными, если a * d = b * c.

Обыкновенная и десятичная дробь — давние друзья. Вот, как они связаны:

• Целая часть десятичной дроби равна целой части смешанной дроби. Если числитель меньше знаменателя, то целая часть равна нулю.
• Дробная часть десятичной дроби содержит те же цифры, что и числитель этой же дроби в обыкновенном виде, если в знаменателе обыкновенной дроби числа 10, 100, 1000 и т. д.
• Количество цифр после запятой зависит от количества нулей в знаменателе обыкновенной дроби, если в знаменателе обыкновенной дроби числа 10, 100, 1000 и т. д. То есть 1 цифра — делитель 10, 4 цифры — делитель 10000.

У нас есть отличные курсы по математике для учеников с 1 по 11 классы, записывайтесь!

Действия с дробями

С дробями можно выполнять те же действия, что и с обычными числами: складывать, вычитать, умножать и делить. А еще дроби можно сокращать и сравнивать между собой. Давайте попробуем.

Сравнение дробей

Из двух дробей с одинаковыми знаменателями больше та, у которой числитель больше.

Сравним 1/5 и 4/5. Как рассуждаем:

 

1. В обеих дробях знаменатель равен 5.


2. В первой дроби числитель равен 1, во второй дроби равен 4.

   1 < 4



3. Поэтому первая дробь 1/5 меньше второй 4/5.
   

Из двух дробей с одинаковыми числителями больше та, у которой знаменатель меньше.

Сравним 1/2 и 1/8. Как рассуждаем:

Представим, что у нас есть торт. Так как знаменатель первой дроби равен 2, то делим торт на две части и забираем себе одну, то есть половину торта.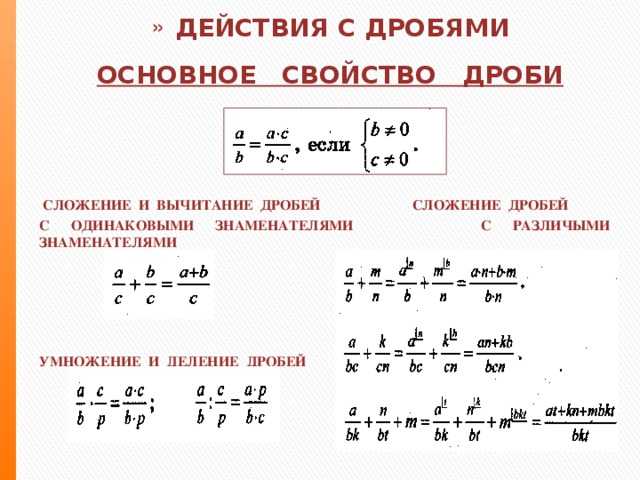

Знаменатель второй дроби равен 8, делим торт на восемь частей и забираем крохотный кусочек. Половина торта больше больше маленького кусочка.

Таким образом 1/2 > 1/8.

Чтобы сравнить дроби с разными знаменателями, нужно привести дроби к общему знаменателю. А после приведения дробей к общему знаменателю, можно применить правило сравнения дробей с одинаковыми знаменателями.

Пример. Сравнить 2/7 и 1/14.

Как рассуждаем:

 

1. Приведем дроби к общему знаменателю:
   
2. Сравним дроби с одинаковыми знаменателями:
   

Ответ: 2/7 > 1/14.

Важно запомнить: любая неправильная дробь больше любой правильной. Потому что неправильная дробь всегда больше или равна 1, а правильная дробь всегда меньше 1.

Чтобы сравнить дроби с разными числителями и знаменателями, нужно:

• привести дроби к общему знаменателю;
• сравнить полученные дроби.

Чтобы привести дроби к общему знаменателю, нужно:

1. Найти общее кратное знаменателей дробей, которое станет их общим знаменателем.


2. Разделить общий знаменатель на знаменатель данных дробей, то есть найти для каждой дроби дополнительный множитель.


3. Умножить числитель и знаменатель каждой дроби на ее дополнительный множитель.

Сокращение дробей

Сокращение дроби — это деление числителя и знаменателя дроби на одно и то же натуральное число. Сократить дробь значит сделать ее короче и проще для восприятия. Например, дробь 1/3 выглядит намного проще и красивее, чем 27/81.

Сокращение дроби выглядит так: зачеркивают числитель и знаменатель, а рядом записывают результаты деления числителя и знаменателя на одно и то же число.

В этом примере делим обе части дроби на двойку.

Можно никуда не спешить и сокращать дроби последовательно, в несколько действий.

Сложение и вычитание дробей

При сложении и вычитании дробей с одинаковыми знаменателями к числителю первой дроби прибавляют числитель второй дроби (из числителя первой вычитают числитель второй) и оставляют тот же знаменатель.

Не забудьте проверить, можно ли сократить дробь и выделить целую часть.

При сложении и вычитании дробей с разными знаменателями нужно найти наименьший общий знаменатель, сложить или вычесть полученные дроби (используем предыдущее правило).

Вот, что делать:

 

1. Найдем наименьшее общее кратное для определения единого делителя.

   Для этого запишем в столбик числа, которые в сумме дают значения делителей. Далее перемножаем полученное и получаем НОК.

   НОК (15, 18) = 3 * 2 * 3 * 5 = 90



2. Найдем дополнительные множители для каждой дроби. Для этого НОК делим на каждый знаменатель:

   90 : 15 = 6,

   90 : 18 = 5.

   Полученные числа запишем справа сверху над числителем.

3. Воспользуемся одним из основных свойств дробей: перемножим числитель и знаменатель на дополнительный множитель. После умножения знаменатель должен быть равен наименьшему общему кратному, которое мы ранее высчитывали. Затем можно перейти к сложению.
   
4. Проверим полученный результат:
   • если числитель больше знаменателя, нужно преобразовать дробь в смешанное число;
   • если есть что сократить, нужно выполнить сокращение.

Ход решения одной строкой:

Сложение или вычитание смешанных чисел можно привести к отдельному сложению их целых частей и дробных частей. Для этого нужно действовать поэтапно:

 

1. Сложить целые части.
   
   


2. Сложить дробные части.
   

   Необходимо приводить к общему, если знаменатели разные. Для этого воспользуемся знаниями из предыдущего примера.



3. Суммировать полученные результаты.
   

Если при сложении дробных частей получилась неправильная дробь, нужно выделить ее целую часть и прибавить к полученной ранее целой части.

Умножение и деление дробей

Произведение двух дробей равно дроби, числитель которой равен произведению числителей, а знаменатель — произведению знаменателей:

Не забываем про сокращение. Это может облегчить вычисления.

Чтобы умножить два смешанных числа, надо:

 

1. преобразовать смешанные дроби в неправильные;


2. перемножить числители и знаменатели дробей;


3. сократить полученную дробь;


4. если получилась неправильная дробь, преобразовать в смешанную.

Чтобы разделить дробь на дробь нужно выполнить следующую последовательность действий:

• числитель первой умножить на знаменатель второй, результат произведения записать в числитель новой дроби;
• знаменатель первой умножить на числитель второй, результат произведения записать в знаменатель новой дроби.

Другими словами это правило звучит так: чтобы разделить одну дробь на другую, надо первую умножить на обратную от второй.

Числа, произведение которых равно 1, называют взаимно обратными.

Как делить дроби с разными знаменателями? На самом деле одинаковые или разные знаменатели у дробей — неважно, потому что все дроби делятся по правилу, описанному выше.

Для деления смешанных чисел необходимо:

• представить числа в виде неправильных дробей;
• разделить то, что получилось друг на друга.

---

---

 

Шпаргалки для родителей по математике

Все формулы по математике под рукой

Лидия Казанцева

Автор Skysmart

К предыдущей статье

417.1K

Параллелограмм: свойства и признаки

К следующей статье

379.4K

Арифметическая прогрессия: свойства и формулы

Получите план обучения, который поможет понять и полюбить математику

На вводном уроке с методистом

1. Выявим пробелы в знаниях и дадим советы по обучению

2. Расскажем, как проходят занятия

3. Подберём курс

Сложение дробей — как складывать дроби 🤔

Поможем понять и полюбить математику

Начать учиться

188. 3K

Тема дробей — одна из самых объемных в математике. Начиная с пятого класса и до самого выпуска из школы эти правила будут пригождаться вновь и вновь. В этой статье разберемся со сложением. Поехали!

Понятие дроби

Дробь — одна из форм записи частного чисел a и b, представленная в виде a/b. Существует два формата записи:

• обыкновенный вид — 1/2 или a/b,
• десятичный вид — 0,5.

Над чертой принято писать делимое, которое является числителем, а под чертой всегда находится делитель, который называют знаменателем. Черта между ними означает деление.

Дроби бывают двух видов:

1. Числовые — состоят из чисел, например, 5/9 или (1,5 − 0,2)/15.

2. Алгебраические — состоят из переменных, например, (x + y)/(x − y). В этом случае значение дроби зависит от данных значений букв.

Дробь называют правильной, когда ее числитель меньше знаменателя. Например, 3/7 и 31/45.

Неправильной называют такую дробь, у которой числитель больше знаменателя или равен ему. Например, 21/4. Такое число является смешанным и читается, как пять целых одна четвертая, а записывается — 5 1/4.

Реши домашку по математике на 5.

Подробные решения помогут разобраться в самой сложной теме.

Основные свойства дробей

Дробь не имеет значения, если делитель равен нулю.

Дробь равняется нулю в том случае, если числитель равен нулю, а знаменатель отличен от нуля.

Дроби a/b и c/d называют равными, если a × d = b × c.

Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится равная ей дробь.

Онлайн-школа Skysmart приглашает детей и подростков на курсы по математике — за интересными задачами, новыми прикладными знаниями и хорошими оценками!

Как плюсовать дроби

Сложение — это арифметическое действие, в результате которого получается новое число. Оно содержит в себе сумму заданных чисел.

Свойства сложения

• От перестановки мест слагаемых сумма не меняется: a + b = b + a.
• Чтобы к сумме двух чисел прибавить третье нужно к первому числу прибавить сумму второго и третьего числа: (a + b) + c = a + (b + c).
• Если к числу прибавить ноль, получится само число: a + 0 = 0 + a = a
• При сложении числа можно переставлять и объединять в группы, результат от этого не изменится.

Давайте рассмотрим несколько вариантов сложения обыкновенных дробей.  

Сложение дробей с одинаковыми знаменателями

Чтобы получить сумму двух дробей с равными знаменателями, нужно сложить числители исходных дробей, а знаменатель оставить прежним.

Не забудьте проверить, можно ли сократить дробь.

Сложение дробей с разными знаменателями

Как складывать дроби с разными знаменателями — для этого нужно найти наименьший общий знаменатель (далее — НОЗ), а затем воспользоваться предыдущим правилом. Вот, что делать:

1. Найдем наименьшее общее кратное знаменателей (далее — НОК) для определения единого делителя.

Для этого записываем в столбик числа, которые в произведении дают значения знаменателей складываемых дробей. Далее перемножаем полученное и получаем НОК.

НОК (15, 18) = 3 × 2 × 3 × 5 = 90

2. Найдем дополнительные множители для каждой дроби. Для этого НОК делим на каждый знаменатель:

• 90 : 15 = 6,
• 90 : 18 = 5.

Полученные числа записываем справа сверху над числителем.

3. Воспользуемся одним из основных свойств дробей: перемножим делимое и делитель на дополнительный множитель. После умножения делитель должен быть равен наименьшему общему кратному, которое мы ранее высчитывали. Затем можно перейти к сложению.

4. Проверим полученный результат:

• если делимое больше делителя, нужно преобразовать в смешанное число;
• если есть что сократить, нужно выполнить сокращение.
  

Еще раз ход решения одной строкой:

Сложение смешанных чисел

Сложение смешанных чисел можно привести к отдельному сложению их целых частей и дробных частей. Для этого нужно действовать поэтапно:

1. Сложить целые части.

2. Сложить дробные части.

Если знаменатели разные, воспользуемся знаниями из предыдущего примера и приведем к общему.

3. Суммируем полученные результаты.

Если при сложении дробных частей получилась неправильная дробь, нужно выделить ее целую часть и прибавить к полученной ранее целой части.

Прибавление и вычитание дробей — смежные темы: принципы и закономерности очень похожи. Чтобы закрепить знания, тренируйтесь решать примеры на сложение дробей как можно чаще.

 

Шпаргалки для родителей по математике

Все формулы по математике под рукой

Лидия Казанцева

Автор Skysmart

К предыдущей статье

Как решать систему неравенств

К следующей статье

198.4K

Деление дробей: теория и практика

Получите план обучения, который поможет понять и полюбить математику

На вводном уроке с методистом

1. Выявим пробелы в знаниях и дадим советы по обучению

2. Расскажем, как проходят занятия

3. Подберём курс

Простой способ вычисления дробей

Понимание дробей (простой способ!)

Дроби

Дроби можно рассматривать как еще один способ увидеть деление.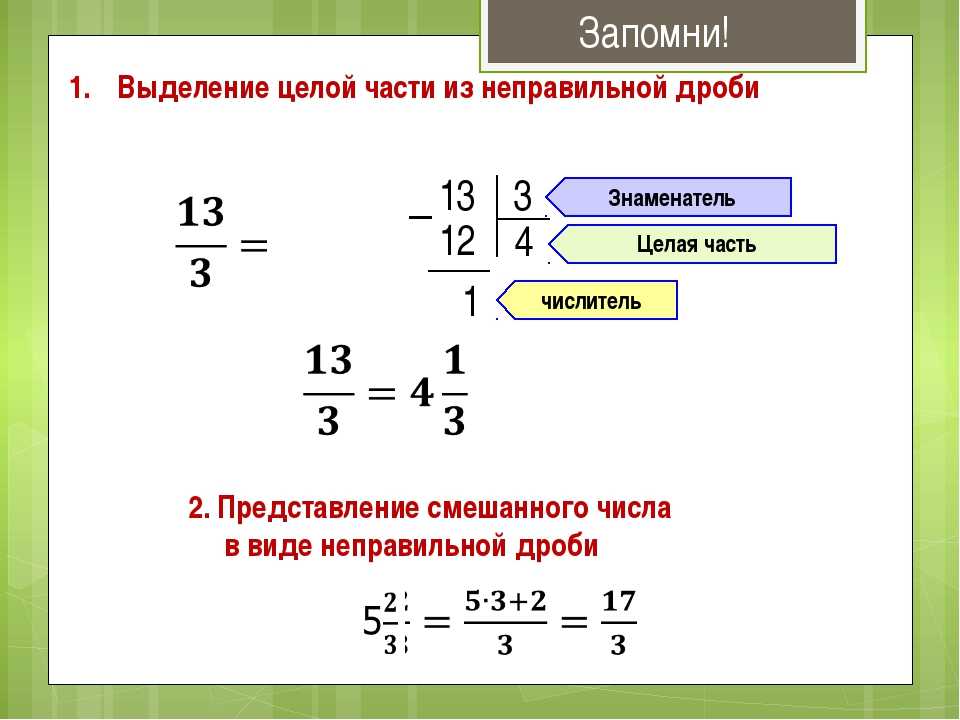 Если у вас есть одна целая пицца и два человека хотят разделить ее поровну, они разделят ее на две половины:

Нижнее число дроби является знаменателем. Он показывает, на сколько частей было разделено целое. В этом случае наша пицца делится на две части.

Правильные дроби, неправильные дроби и смешанные числа

Правильная дробь – это та, у которой числитель меньше знаменателя.

Неправильная дробь – это та, у которой числитель больше знаменателя. Если числитель больше знаменателя, то дробь равна числу больше единицы.

Самые низкие условия

Нахождение GCF (наибольшего общего делителя)

Наибольший общий делитель — это наибольший делитель, который делит два числа. Мы находим это, выясняя, какие простые числа перемножаются, чтобы составить каждое число. Простое число — это число, которое можно разделить только само на себя или на единицу. Примеры простых чисел: 1, 2, 3, 5, 7, 11, 13, 17, 19., 23, 29 и т. д. Мы хотим сосредоточиться на тех, которые меньше десяти в большинстве случаев.

Хотите узнать больше? Почему бы не пройти онлайн-курс по базовой математике?

Определение ЖК-дисплея (наименьший общий знаменатель)

 

Сложение и вычитание дробей

Чтобы сложить или вычесть две дроби, у двух дробей должен быть один и тот же знаменатель. Поэтому вам придется найти наименьший общий знаменатель и заменить каждую дробь эквивалентной дробью. Затем вы добавляете или вычитаете числители, как указано, и ставите полученное число над знаменателем и сокращаете дробь до наименьших членов.

Умножение и деление дробей

Умножать дроби довольно просто. Для начала вы можете поместить каждую фракцию в самое низкое значение. Затем умножьте числители, чтобы получить числитель, и умножьте знаменатели, чтобы получить новый знаменатель. И уменьшите или упростите дробь, чтобы выразить ее в самом низком значении. Если вы умножаете дробь на целое число, положите целое число на единицу, чтобы получить дробь.

Примеры:

Пять раз 4/5: Положите пять на единицу, затем умножьте 5 x 4, чтобы получить 20, и 1 x 5, чтобы получить 5. Двадцать можно разделить на 5, чтобы получить ответ 4.

Обратные дроби

Произведение числа и его обратного числа равно 1.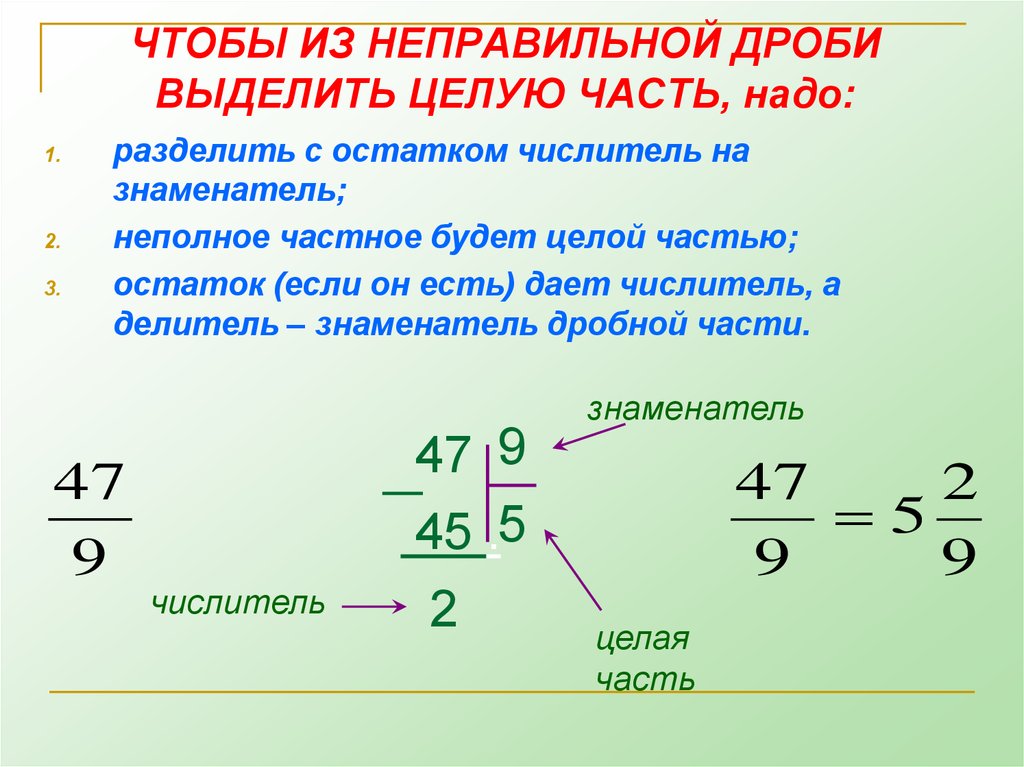

Знаки и дроби

Если знаменатель или числитель отрицательные, дробь считается отрицательной дробью. Если и знаменатель, и числитель отрицательные, дробь считается положительной.

Сложение двух дробей одного знака (положительного или отрицательного) дает ответ с тем же знаком. Возможно, вам придется сначала привести дроби к общему знаменателю.

Сложение дробей

PGSG8gJWt1g

Дробь вроде 3 4 говорит, что у нас есть 3 из 4 частей, на которые делится целое.

Чтобы сложить дроби, нужно выполнить три простых шага:

• Шаг 1: убедитесь, что нижние числа ( знаменатели ) совпадают
• Шаг 2: Сложите верхние числа ( числители ), поместите этот ответ над знаменателем
• Шаг 3. Упростите дробь (если возможно)

Пример:

1 ​​ 4 + 1 ​​ 4

Шаг 1 . Нижние числа (знаменатели) уже одинаковы. Сразу переходите к шагу 2.

Шаг 2 . Сложите верхние числа и поставьте ответ над тем же знаменателем:

.

1 ​​ 4 + 1 ​​ 4 «=» 1 ​​+ 1 4 «=» 2 4

Шаг 3 . Упростите дробь:

2 4 «=» 1 ​​ 2

На картинке это выглядит так:

1 ​​ 4	+	1 ​​ 4	=	2 4	=	1 ​​ 2

. .. и вы видите, как 2 4 проще, как 1 ​​ 2 ? (см. Эквивалентные дроби.)

 

Пример:

1 ​​ 3 + 1 ​​ 6

Шаг 1 : Нижние числа разные. Видите, как кусочки разного размера?

1 ​​ 3	+	1 ​​ 6	=	?

Нам нужно сделать их одинаковыми, прежде чем мы сможем продолжить, потому что мы не можем добавить их вот так.

Число «6» в два раза больше «3», поэтому, чтобы сделать нижние числа одинаковыми, мы можем умножить верхнюю и нижнюю часть первой дроби на 9. 0164 2 , вот так:

× 2

1 ​​ 3

=

2 6

× 2

Важно: вы умножаете сверху и снизу на одинаковую величину,
чтобы значение дроби осталось прежним

Теперь дроби имеют одинаковое нижнее число («6»), и наш вопрос выглядит так:

2 6	+	1 ​​ 6

Нижние числа теперь одинаковы, поэтому мы можем перейти к шагу 2.

 

Шаг 2 : Сложите верхние числа и поместите их над одним и тем же знаменателем:

2 6 + 1 ​​ 6 «=» 2 + 1 6 «=» 3 6

На картинке это выглядит так:

2 6	+	1 ​​ 6	=	3 6

Шаг 3 : Упростить дробь:

3 6 «=» 1 ​​ 2

 

В графической форме весь ответ выглядит так:

2 6	+	1 ​​ 6	=	3 6	=	1 ​​ 2

 

С ручкой и бумагой

А вот как это сделать ручкой и бумагой (нажмите кнопку воспроизведения):

 

Играй! Попробуйте сложить дроби.

Стихотворение, которое поможет вам вспомнить

♫ «Если вашей целью является сложение или вычитание,
нижние числа должны совпадать!
♫ «Измените низ, используя умножение или деление,
Но то же самое нужно применить и к верху,
♫ «И не забудьте упростить,
Пока не пришло время прощаться»

Пример:

1 ​​ 3 + 1 ​​ 5

Опять же, нижние цифры разные (ломтики разного размера)!

1 ​​ 3	+	1 ​​ 5	=	?

Но давайте попробуем разделить их на более мелкие, чтобы были одинаковыми :

5 15	+	3 15

Первая дробь: умножив верх и низ на 5, мы получили 5 15 :

× 5

1 ​​ 3

=

5 15

× 5

Вторая дробь: умножив верх и низ на 3, мы получили 3 15 :

× 3

1 ​​ 5

=

3 15

× 3

Нижние числа теперь одинаковы, поэтому мы можем добавить верхние числа:

5 15	+	3 15	=	8 15

Результат уже настолько прост, насколько это возможно, поэтому ответ: 

1 ​​ 3 + 1 ​​ 5 «=» 8 15

Делаем знаменатели одинаковыми

Откуда в предыдущем примере мы узнали, что нужно разрезать их на ¹ / ₁₅ тысяч, чтобы знаменатели совпадали? Мы просто перемножили два знаменателя (3 × 5 = 15).

Прочитать о двух основных способах приведения знаменателей в соответствие можно здесь:

• Метод общего знаменателя, или
• Метод наименьшего общего знаменателя

Они оба работают, используйте тот, который вам больше нравится!

Пример: Кексы

Вы хотите испечь и продать кексы:

• Друг может предоставить ингредиенты, если вы дадите им ¹ / ₃ продаж
• Прилавок на рынке стоит ¹ / ₄ продаж

Сколько это вообще?

 

Нам нужно добавить ¹ / ₃ и ¹ / ₄

1 ​​ 3 + 1 ​​ 4 = ? ?

Сначала сделайте нижние числа (знаменатели) одинаковыми.

Умножить верх и низ ¹ / ₃ на 4 :

1×4 3×4 + 1 ​​901 56 4 = ? ?

И умножить верх и низ ¹ / ₄ на 3 :

1×4 3×4 + 1×3 4×3 = ? ?

Теперь делаем вычисления:

4 12 + 3 12 = 4+3 9015 6 12 = 7 12

 

Ответ: 7 12 сбываний идут в ингридиентах и ​​ценах рынка.