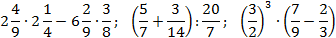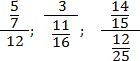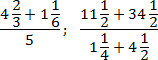Действия с дробями, подробно с примерами

Действия с дробями. В этой статье разберём примеры, всё подробно с пояснениями. Рассматривать будем обыкновенные дроби. В дальнейшем разберём и десятичные. Рекомендую посмотреть весь список материалов и изучать последовательно.

1. Сумма дробей, разность дробей.

Правило: при сложении дробей с равными знаменателями, в результате получаем дробь – знаменатель которой остаётся тот же, а числитель её будет равен сумме числителей дробей.

Правило: при вычислении разности дробей с одинаковыми знаменателями получаем дробь  – знаменатель остаётся тот же, а из числителя первой дроби вычитается числитель второй.

Формальная запись суммы и разности дробей с равными знаменателями:

Примеры (1):

Понятно, что когда даны обыкновенные дроби, то всё просто, а если смешанные? Ничего сложного…

Вариант 1 – можно перевести их в обыкновенные и далее вычислять.

Вариант 2 – можно отдельно «работать» с целой и дробной частью.

Примеры (2):

Ещё:

А если будет дана разность двух смешанных дробей и числитель первой дроби будет меньше числителя второй? Тоже можно действовать двумя способами.

Примеры (3):

*Перевели в обыкновенные дроби, вычислили разность, перевели полученную неправильную дробь в смешанную.

*Разбили на целые и дробные части, получили тройку, далее представили 3 как сумму 2 и 1, при чём единицу представили как 11/11, далее нашли разность 11/11 и 7/11 и вычислили результат. Смысл изложенных преобразований заключается в том, чтобы взять (выделить) единицу и представить её в виде дроби с нужным нам знаменателем, далее от этой дроби мы уже можем вычесть другую.

Ещё пример:

 

Вывод: имеется универсальный подход  – для того, чтобы вычислить сумму (разность) смешанных дробей с равными знаменателями их всегда можно перевести в неправильные, далее выполнить необходимое действие. После этого если в результате получаем неправильную дробь переводим её в смешанную.

Выше мы рассмотрели примеры с дробями, у которых равные знаменатели.  А если знаменатели будут отличаться? В этом случае дроби приводятся к одному знаменателю и выполняется указанное действие. Для изменения (преобразования) дроби используется основное свойство дроби.

Рассмотрим простые примеры:

В данных примерах мы сразу видим каким образом можно преобразовать одну из дробей, чтобы получить равные знаменатели.

Если обозначить способы приведения дробей к одному знаменателю, то этот назовём СПОСОБ ПЕРВЫЙ.

То есть, сразу при «оценке» дроби нужно прикинуть сработает ли такой подход – проверяем делится ли больший знаменатель на меньший. И если делится, то выполняем преобразование — домножаем числитель и знаменатель так чтобы у обеих дробей знаменатели стали равными.

Теперь посмотрите на эти примеры:

К ним указанный подход не применим. Существуют ещё способы приведения дробей к общему знаменателю, рассмотрим их.

Способ ВТОРОЙ.

Умножаем числитель и знаменатель первой дроби на знаменатель второй, а числитель и знаменатель второй дроби на знаменатель первой:

*Фактически мы приводим дроби к виду, когда знаменатели становятся равными. Далее используем правило сложения робей с равными знаменателями.

Пример:

*Данный способ можно назвать универсальным, и он работает всегда. Единственный минус в том, что после вычислений может получится дробь которую необходимо будет ещё сократить.

Рассмотрим пример:

Видно что числитель и знаменатель делится на 5:

Способ ТРЕТИЙ.

Необходимо найти наименьшее общее кратное (НОК) знаменателей. Это и будет общий знаменатель. Что это за число такое? Это наименьшее натуральное число, которое делится на каждое из чисел.

Посмотрите, вот два числа: 3 и 4, есть множество чисел, которые делятся на них – это 12, 24, 36, … Наименьшее из них 12. Или 6 и 15, на них делятся 30, 60, 90 …. Наименьшее 30. Вопрос – а как определить это самое наименьшее общее кратное?

Имеется чёткий алгоритм, но часто это можно сделать и сразу без вычислений. Например, по указанным выше примерам (3 и 4, 6 и 15) никакого алгоритма не надо, мы взяли большие числа (4 и 15) увеличили их в два раза и увидели, что они делятся на второе число, но  пары чисел могут быть и другими, например 51 и 119.

Алгоритм. Для того, чтобы определить наименьшее общее кратное нескольких чисел, необходимо:

— разложить каждое из чисел на ПРОСТЫЕ множители

— выписать разложение БОЛЬШЕГО из них

— умножить его на НЕДОСТАЮЩИЕ множители других чисел

Рассмотрим примеры: 

50 и 60   =>  50 = 2∙5∙5    60 = 2∙2∙3∙5

в разложении большего числа не хватает одной пятёрки

 =>   НОК(50,60) = 2∙2∙3∙5∙5 = 300

48 и 72   =>   48 = 2∙2∙2∙2∙3    72 = 2∙2∙2∙3∙3            

в разложении большего числа не хватает двойки и тройки

=>   НОК(48,72) = 2∙2∙2∙2∙3∙3 = 144

* Наименьшее общее кратное двух простых чисел равно их произведению

Вопрос! А чем полезно нахождение наименьшего общего кратного, ведь можно пользоваться вторым способом и полученную дробь просто сократить? Да, можно, но это не всегда удобно. Посмотрите, какой получится знаменатель для чисел 48 и 72, если их просто перемножить 48∙72 = 3456. Согласитесь, что приятнее работать с меньшими числами.

Рассмотрим примеры:

*51 = 3∙17    119 = 7∙17

в разложении большего числа не хватает тройки

 =>   НОК(51,119) = 3∙7∙17

А теперь применим первый способ:

*Посмотрите какая разница в вычислениях, в первом случае их минимум, а во втором нужно потрудиться отдельно на листочке, да ещё и дробь которую получили сократить необходимо. Нахождение НОК упрощает работу значительно.

Ещё примеры:

*Во втором примере и так видно, что наименьшее число, которое делится на 40 и 60 равно 120.

ИТОГ! ОБЩИЙ АЛГОРИТМ ВЫЧИСЛЕНИЙ!

— приводим дроби к обыкновенным, если есть целая часть.

— приводим дроби к общему знаменателю (сначала смотрим делится ли один знаменатель на другой, если делится то умножаем числитель и знаменатель этой другой дроби; если не делится действуем посредством других указанных выше способов).

— получив дроби с равными знаменателями, выполняем действия (сложение, вычитание).

— если необходимо, то результат сокращаем.

— если необходимо, то выделяем целую часть.

2. Произведение дробей.

Правило простое. При умножении дробей умножаются их числители и знаменатели:

Примеры:

Если есть возможность сократить дробь на стадии вычисления, то лучше это сделать:

Ещё правило относящееся к умножению!

Примеры, которые мы уже рассмотрели:

Определить, сколько составляет 3/7 от числа 63?

Задача. Весь путь составляет 180 километров. Турист в первый день прошёл 3/10 пути. Сколько километров турист прошёл в первый день?

Задача. На базу привезли 13 тонн овощей. Картофель составляет ¾ от всех завезённых овощей. Сколько килограмм  картофеля завезли на базу?

С произведением закончим.

*Ранее обещал вам привести формальное объяснение основного свойства дроби через произведение, пожалуйста:

3. Деление дробей.

Деление дробей сводится к их умножению. Здесь важно запомнить, что дробь являющаяся делителем (та, на которую делят) переворачивается и действие меняется на умножение:

Данное действие может быть записано в виде так называемой четырёхэтажной дроби, ведь само деление «:» тоже можно записать как дробь:

Примеры:

На этом всё! Успеха вам!

С уважением, Александр Крутицких.

Делитесь информацией в социальных сетях.

Как решать дроби. Решение дробей.

В статье покажем, как решать дроби на простых понятных примерах. Разберемся, что такое дробь и рассмотрим решение дробей!

Понятие дроби вводится в курс математики начиная с 6 класса средней школы.

Дроби имеют вид : ±X/Y, где Y — знаменатель, он сообщает на сколько частей разделили целое, а X — числитель, он сообщает, сколько таких частей взяли. Для наглядности возьмем пример с тортом:

В первом случае торт разрезали поровну и взяли одну половину, т.е. 1/2. Во втором случае торт разрезали на 7 частей, из которых взяли 4 части, т.е. 4/7.

Если часть от деления одного числа на другое не является целым числом, ее записывают в виде дроби.

Например, выражение 4:2 = 2 дает целое число, а вот 4:7 нацело не делится, поэтому такое выражение записывается в виде дроби 4/7.

Иными словами дробь — это выражение, которое обозначает деление двух чисел или выражений, и которое записывается с помощью дробной черты.

Если числитель меньше знаменателя — дробь является правильной, если наоборот — неправильной. В состав дроби может входить целое число.

Например, 5 целых 3/4.

Данная запись означает, что для того, чтобы получить целую 6 не хватает одной части от четырех.

Если вы хотите запомнить, как решать дроби за 6 класс, вам надо понять, что решение дробей, в основном, сводится к понимаю нескольких простых вещей.

• Дробь по сути это выражение доли. То есть числовое выражение того, какую часть составляет данное значение от одного целого. К примеру дробь 3/5 выражает, что, если мы поделили что то целое на 5 частей и количество долей или частей это этого целого — три.
• Дробь может быть меньше 1, например 1/2(или по сути половина), тогда она правильная. Если дробь больше 1, к примеру 3/2(три половины или один с половиной), то она неправильная и для упрощения решения, нам лучше выделить целую часть 3/2= 1 целая 1/2.
• Дроби это такие же числа, как 1, 3, 10, и даже 100, только числа это не целые а дробные. С ними можно выполнять все те же операции, что с числами. Считать дроби не сложнее, и далее на конкретных примерах мы это покажем.

Как решать дроби. Примеры.

К дробям применимы самые разные арифметические операции.

Приведение дроби к общему знаменателю

Например, необходимо сравнить дроби 3/4 и 4/5.

Чтобы решить задачу, сначала найдем наименьший общий знаменатель, т.е. наименьшее число, которое делится без остатка на каждый из знаменателей дробей

Наименьший общий знаменатель(4,5) = 20

Затем знаменатель обоих дробей приводится к наименьшему общему знаменателю

Ответ: 15/20

Сложение и вычитание дробей

Если необходимо посчитать сумму двух дробей, их сначала приводят к общему знаменателю, затем складывают числители, при этом знаменатель останется без изменений. Разность дробей считается аналогичным образом, различие лишь в том, что числители вычитаются.

Например, необходимо найти сумму дробей 1/2 и 1/3

Ответ: 5/6

Теперь найдем разность дробей 1/2 и 1/4

Ответ: 1/4

Умножение и деление дробей

Тут решение дробей несложное, здесь все достаточно просто:

• Умножение — числители и знаменатели дробей перемножаются между собой;
• Деление — сперва получаем дробь, обратную второй дроби, т.е. меняем местами ее числитель и знаменатель, после чего полученные дроби перемножаем.

Например:

На этом о том, как решать дроби, всё. Если у вас остались какие то вопросы по решению дробей, что то непонятно, то пишите в комментарии и мы обязательно вам ответим.

Для закрепления материала рекомендуем также посмотреть наше видео:

Также рекомендуем к использованию наш онлайн калькулятор дробей!

В нем вы можете посмотреть, как строить решение, на собственных примерах.

Если вы учитель , то возможно скачать презентацию для начальной школы (http://school-box.ru/nachalnaya-shkola/prezentazii-po-matematike.html) будет вам кстати.

---

Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:

---

Сложные выражения с дробями. Порядок действий

8 августа 2011

Теперь, когда мы научились складывать и умножать отдельные дроби, можно рассматривать более сложные конструкции. Например, что, если в одной задаче встречается и сложение, и вычитание, и умножение дробей?

В первую очередь, надо перевести все дроби в неправильные. Затем последовательно выполняем требуемые действия — в том же порядке, как и для обычных чисел. А именно:

1. Сначала выполняется возведение в степень — избавьтесь от всех выражений, содержащих показатели;
2. Затем — деление и умножение;
3. Последним шагом выполняется сложение и вычитание.

Разумеется, если в выражении присутствуют скобки, порядок действий изменяется — все, что стоит внутри скобок, надо считать в первую очередь. И помните о неправильных дробях: выделять целую часть надо лишь тогда, когда все остальные действия уже выполнены.

Задача. Найдите значения выражений:

Переведем все дроби из первого выражения в неправильные, а затем выполним действия:

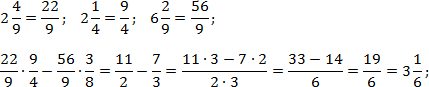
Теперь найдем значение второго выражения. Тут дробей с целой частью нет, но есть скобки, поэтому сначала выполняем сложение, и лишь затем — деление. Заметим, что 14 = 7 · 2. Тогда:

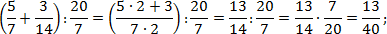
Наконец, считаем третий пример. Здесь есть скобки и степень — их лучше считать отдельно. Учитывая, что 9 = 3 · 3, имеем:

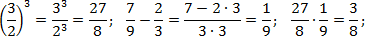
Обратите внимание на последний пример. Чтобы возвести дробь в степень, надо отдельно возвести в эту степень числитель, и отдельно — знаменатель.

Можно решать по-другому. Если вспомнить определение степени, задача сведется к обычному умножению дробей:

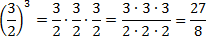
Многоэтажные дроби

До сих пор мы рассматривали лишь «чистые» дроби, когда числитель и знаменатель представляют собой обыкновенные числа. Это вполне соответствует определению числовой дроби, данному в самом первом уроке.

Но что, если в числителе или знаменателе разместить более сложный объект? Например, другую числовую дробь? Такие конструкции возникают довольно часто, особенно при работе с длинными выражениями. Вот пара примеров:

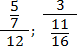
Здесь и далее мы будем называть эти дроби многоэтажными. Однако имейте в виду, что общепризнанного названия у них нет, и в разных учебниках могут встречаться другие определения.

Правило работы с многоэтажными дробями всего одно: от них надо немедленно избавляться. Удалить «лишние» этажи довольно просто, если вспомнить, что дробная черта означает стандартную операцию деления. Поэтому любую дробь можно переписать следующим образом:

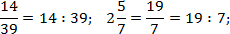
Пользуясь этим фактом и соблюдая порядок действий, мы легко сведем любую многоэтажную дробь к обычной. Взгляните на примеры:

Задача. Переведите многоэтажные дроби в обычные:

В каждом случае перепишем основную дробь, заменив разделительную черту знаком деления. Также вспомним, что любое целое число представимо в виде дроби со знаменателем 1. Т.е. 12 = 12/1; 3 = 3/1. Получаем:

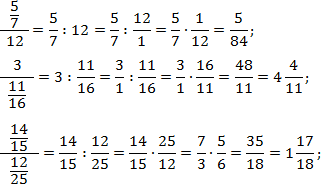
В последнем примере перед окончательным умножением дроби были сокращены.

Специфика работы с многоэтажными дробями

В многоэтажных дробях есть одна тонкость, которую всегда надо помнить, иначе можно получить неверный ответ, даже если все вычисления были правильными. Взгляните:

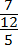
Это выражение можно прочитать по-разному:

1. В числителе стоит отдельное число 7, а в знаменателе — дробь 12/5;
2. В числителе стоит дробь 7/12, а в знаменателе — отдельное число 5.

Итак, для одной записи получили две совершенно разных интерпретации. Если подсчитать, ответы тоже будут разными:

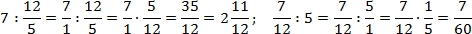
Чтобы запись всегда читалась однозначно, используйте простое правило: разделяющая черта основной дроби должна быть длиннее, чем черта вложенной. Желательно — в несколько раз.

Если следовать этому правилу, то приведенные выше дроби надо записать так:

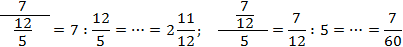
Да, возможно, это некрасиво и занимает слишком много места. Зато вы будете считать правильно. Напоследок — пара примеров, где действительно возникают многоэтажные дроби:

Задача. Найдите значения выражений:

Итак, работаем с первым примером. Переведем все дроби в неправильные, а затем выполним операции сложения и деления:

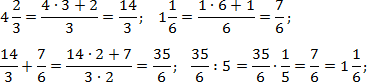
Аналогично поступим со вторым примером. Переведем все дроби в неправильные и выполним требуемые операции. Чтобы не утомлять читателя, я опущу некоторые очевидные выкладки. Имеем:

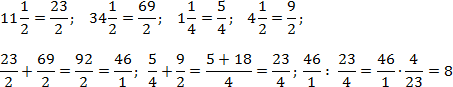
Благодаря тому, что в числителе и знаменателе основных дробей стоят суммы, правило записи многоэтажных дробей соблюдается автоматически. Кроме того, в последнем примере мы намеренно оставили число 46/1 в форме дроби, чтобы выполнить деление.

Также отмечу, что в обоих примерах дробная черта фактически заменяет скобки: первым делом мы находили сумму, и лишь затем — частное.

Кто-то скажет, что переход к неправильным дробям во втором примере был явно избыточным. Возможно, так оно и есть. Но этим мы страхуем себя от ошибок, ведь в следующий раз пример может оказаться намного сложнее. Выбирайте сами, что важнее: скорость или надежность.

Смотрите также:

1. Умножение и деление дробей
2. Тест к уроку «Сложные выражения с дробями» (легкий)
3. Тест к уроку «Округление с избытком и недостатком» (1 вариант)
4. Что такое ЕГЭ по математике 2011 и как его сдавать
5. Периодические десятичные дроби
6. Задача B5: метод узлов

Дроби, операции с дробями | umath.ru

Дробь — форма представления числа в математике. Дробная черта обозначает операцию деления. Числителем дроби называется делимое, а знаменателем — делитель. Например, в дроби 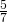числителем является число 5, а знаменателем — 7.

Правильной называется дробь, у которой модуль числителя больше модуля знаменателя. Если дробь является правильной, то модуль её значения всегда меньше 1. Все остальные дроби являются неправильными.

Дробь называют смешанной, если она записана как целое число и дробь. Это то же самое, что и сумма этого числа и дроби:

   

Основное свойство дроби

Если числитель и знаменатель дроби умножить на одно и то же число, то значение дроби не изменится, то есть, например,

   

Приведение дробей к общему знаменателю

Чтобы привести две дроби к общему знаменателю, нужно:

1. Числитель первой дроби умножить на знаменатель второй
2. Числитель второй дроби умножить на знаменатель первой
3. Знаменатели обеих дробей заменить на их произведение

Действия с дробями

Сложение. Чтобы сложить две дроби, нужно

1. Привести дроби к общему знаменателю
2. Сложить новые числители обеих дробей, а знаменатель оставить без изменений

Пример:

   

Вычитание. Чтобы вычесть одну дробь из другой, нужно

1. Привести дроби к общему знаменателю
2. Вычесть из числителя первой дроби числитель второй, а знаменатель оставить без изменений

Пример:

   

Умножение. Чтобы умножить одну дробь на другую, следует перемножить их числители и знаменатели:

   

Деление. Чтобы разделить одну дробь на другую, следует числитель первой дроби умножить на знаменатель второй, а знаменатель первой дроби умножить на числитель второй:

   

Как делать дробь для охоты своими руками: оборудование, инструкции

Охота считается достаточно затратным занятием, особенно для начинающих стрелков. Причина тому — отсутствие опыта, что отражается на точности попаданий. В связи с этим новичку, чтобы пристреляться, потребуется израсходовать довольно большое количество дроби. Стоят дробовые боеприпасы немало. Единственный выход – это научиться самому готовить охотничью дробь. Судя по отзывам, ничего сложного в этом деле нет. При наличии соответствующего оборудования справиться с задачей можно и в домашних условиях. О том, как сделать своими руками дробь для охоты, вы узнаете из данной статьи.

Самый простой способ

Данный метод подойдет для тех, кто не хочет возиться с изготовлением специальной конструкции для литья. Ограничиться можно несколькими кирпичами или металлическими подпорками, консервной банкой и емкостью с водой. Делать дробь таким способом достаточно просто. В банку засыпается небольшое количество свинца. Затем ее нужно расположить над огнем. На кирпичи кладут стальную сетку, а сверху на нее ставят банку. Также ее можно подвесить при помощи проволоки. Что ему предпринять, мастер решает исходя из своих возможностей. У самого края банки делают небольшое отверстие, через которое будет выливаться свинец. Емкость с водой обтягивают фланелью.

При помощи сковородки

Тем, кого интересует, как делать дробь, можно посоветовать еще один способ литья при помощи подручных средств. Судя по отзывам, в итоге получаются довольно неплохие дробинки пятого номера. Как смастерить своими руками дроболейку? Что для этого понадобится? Перед тем как отлить дробь, домашнему умельцу нужно приготовить старую ненужную сковородку, тазик или другую подобную емкость, магнит, водопроводную воду и свинец из кабеля или аккумулятора. Прежде чем приступить, на дне сковородки, у самого ее края, сверлится отверстие. Диаметр его должен составить 0,7 мм. Далее в это отверстие необходимо вставить временную заглушку.

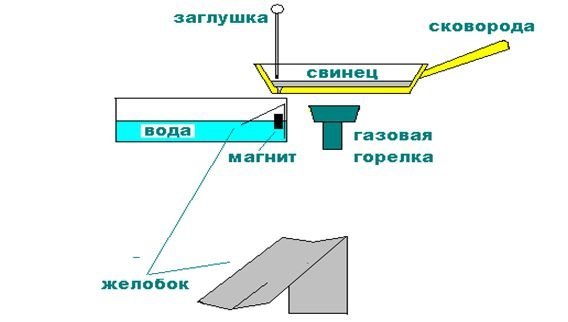
Можно воспользоваться гвоздем или стальной проволокой соответствующего диаметра. Лишь после выполнения этих действий приступают непосредственно к литью свинца.

Как делать дробь?

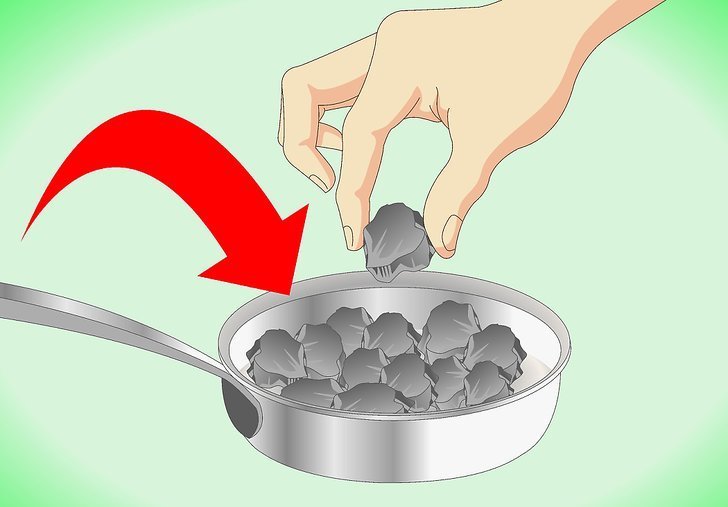
Готовят «начинку» для охотничьего боеприпаса следующим образом. Сначала ставят сковородку на газ и кладут в нее кусочки свинца. Желательно, чтобы их общий вес не превышал 3 кг.

Затем приготовленный таз наполняется водой. Сама емкость ставится внизу, под сковородой, на отдалении в пару сантиметров. Далее посредством магнита к тазику крепится желобок, который предварительно обтягивают шелком или фланелью и хорошенько намачивают. Когда свинец растопится, заглушку следует вынуть. Таким образом, металл приобретет соответствующую форму. Далее он будет стекать из отверстия в сковородке по желобку в воду и там остывать.

О размере дробинок

Кроме вопроса, как делать дробь, новичков интересует, от чего может зависеть величина заряда. Прежде всего на размер дробинки влияет диаметр отверстия, через которое вытекает расплавленный свинец. Кроме того, большое значение имеет интенсивность нагрева.

Например, если мастер хочет сделать крупную дробь, но расширять отверстие в сковороде не планирует, то ему достаточно немного уменьшить огонь. В итоге свинец будет вытекать медленнее, от чего дробь получится крупной.

Об изготовлении в ведре

Данный способ подойдет для тех мастеров, у которых нет газовой плиты или паяльной лампы. Весь процесс будет происходить в ведре. Также для растопки свинца понадобится консервная банка, которую предварительно необходимо оснастить отверстием в 1,5 мм. Как утверждают специалисты, такой диаметр на выходе даст дробь седьмого номера. При необходимости отверстие будет нетрудно расширить при помощи обычного сверла или швейной иглы. Сначала ведро наполовину необходимо заполнить холодной водой. Далее в него помещается емкость со свинцом (кастрюля или банка). Монтаж осуществляется с помощью металлических прутков. Важно, чтобы от днища банки до поверхности воды соблюдалась дистанция не более 5 см.

Выполнив все необходимые замеры, данную емкость извлекают, а ведро наполняют соляркой (в пределах 3-4 л). Специалисты рекомендуют производить плавку аккумуляторного и чистого свинца в пропорции 50:50. Добавлять его в емкость желательно постепенно. Если переборщить, то в банке образуется большое давление, отчего в дробинках появятся хвостики. После того как банка установлена, поджигается содержимое ведра. Для этого смачивают горючим тряпку, осторожно поджигают и бросают в солярку. Спустя некоторое время нужно легонько постукивать по таре со свинцом. Это необходимо для того, чтобы он начал вытекать из отверстия. Преодолев слой горящей солярки, уже сформированная дробинка попадает в воду, где и окончательно остывает.

Альтернативный способ

Может быть так, что у домашнего умельца нет возможности сделать своими руками дроболейку. В таком случае ему придется воспользоваться сухим камышом. Желательно, чтобы его толщина соответствовала толщине требуемых дробинок. Сам камыш аккуратно разрезается пополам. Сначала свинец растапливается в какой-нибудь емкости. Далее им заполняют половинки камыша. После остывания дробинки нарезаются из полученной свинцовой полоски. Как делать дробь, если камыша нет под рукой? В таком случае можно порекомендовать вырезать ножом в деревянной поверхности несколько канавок. Какую они будут иметь глубину, мастер решает исходя из того, какой размер дроби он хочет получить. Куски свинца, так же как и в первом случае, вначале растапливаются, а затем металл заливают в эти канавки. Должна получиться свинцовая проволока, из которой и будет нарезаться дробь.

Завершающий этап

Какой бы способ плавки свинца ни избрал бы домашний умелец, в самом конце дробинки следует обработать. Суть данной процедуры — в сортировке, утряске и шлифовке. Чтобы убрать ненужный шлак, вначале дробь просеивают при помощи специального сита. С целью избавить изделия от твердых вкраплений осуществляют обкатку. Шлифовка и утряска выполняются с добавлением графитового порошка в отдельной емкости, которую следует плотно закупорить. Судя по многочисленным отзывам, самодельная дробь по своему внешнему виду и убойности не будет отличаться от заводской.

как сделать дробь в домашних условиях

Опубликовано 28 Сен 2017. Автор: master

Купить свинцовую охотничью дробь можно в специализированных магазинах «Охотник». Однако, производство охотничьей дроби не сложно наладить самому. Причем мне известно два принципиально различных способа изготовления этого необходимого для охоты элемента.
Итак, как сделать дробь в домашних условиях.
Изготовление охотничьей дроби

Первый способ: литье.

Расплавленный свинец льют (капают) в солярку или масло (можно в воду, но не желательно). Лить расплав нужно через отверстие, диаметр которого равен диаметру дроби, которую вы хотите получить. Подробнее все выглядит так: берется старая пустая консервная банка и в ней пробивается отверстие нужного диаметра. Затем расплавляется свинец и льется через это отверстие в солярку или воду. Но при этом способе не получится качественной дроби. Шарики будут получаться с «хвостиками», то есть в виде капельки. Экспериментируя с высотой, с которой капают свинец, можно получить очень маленькие «хвостики».

Второй способ: катание.

Он более трудоемкий, но в этом случае дробь получается почти как заводская. Я пользуюсь именно этим способом. Опишу его на примере изготовления дроби «00». Дробь этой марки можно использовать и для стрельбы из пневматического оружия. Катание дроби осуществляется так называемым «блином» в «сковороде». Изготовление этого приспособления оставлю за рамками статьи, сказав лишь, что масса «блина» должна быть порядка 5— 7 кг. Для катания используются заготовки в виде цилиндриков из свинца, у которых диаметр равен высоте. Это непременное условие. Для расчета этих необходимых параметров я исхожу из диаметра дробины, которую хочу получить.
У дроби «00» диаметр равен 4,5 мм. Согласно равенству объемов цилиндра и шара получаю зависимость: Дц=0,91хДш. Из этой формулы получаю, что для изготовления необходимой нам дроби нужны цилиндрики с диаметром и высотой равными приблизительно 4,1 мм.
Для получения цилиндриков я сначала отливаю из свинца палочки нужного диаметра. Для этого я беру проволоку диаметром 4 мм, на нее наматываю алюминиевую фольгу и получаю трубочки необходимого мне диаметра, длина их должна быть примерно равна 200 мм. Затем в эти трубочки заливаем свинец. Для того чтобы они находились в вертикальном положении, их можно воткнуть в песок. Полученные таким образом палочки нужно порезать на цилиндрики. Для этого изготавливают резак. Его конструкция произвольна и подобна резаку для фотобумаги с тем дополнением, что в нем установлен ограничитель подачи, который сам автоматически отмеряет длину цилиндрика, которую вы сами устанавливаете. Полученные таким образом заготовки засыпают в «сковороду», закрывают «блином» и обрабатывают посредством вращения «блина» в «сковороде» относительно центральной оси до получения шариков. Чем дольше вы катаете дробь, тем качественнее она получается.
Для катания лучше использовать свинец, который применяют для производства антикоррозийного покрытия кабелей (силовых, телефонных и других). Но можно и аккумуляторный, хотя он более жесткий.
Для того чтобы дробь была совсем как заводская и не освинцовывала стволы, ее покрывают графитом, для этого в пустую бутылку насыпают дроби примерно до половины и добавляют немного графита (размолотого грифеля от карандаша или центрального стержня от батарейки). И трясут некоторое время.

Дробь охотничья какой номер на какую дичь

• Перепелов, бекасов, дупелей и прочих мелких куликов рекомендуется бить 8, 9 и 10 номерами.
• Куропаток, чирков, вальдшнепов, рябчиков возьмет уже 6 или 7 номер.
• Тетеревов, уток, диких голубей и фазанов поможет добыть 5 и 6 номер.
• Уток, зайцев, глухарей, гусей стреляют 2, 1, 0 номером.
• Лисица, волк, косуля – 00, 000, 0000 номер.

Таблица охотничьей дроби

Дробь                    Размер
Дробь 0000 (4/0) размер 5 мм диаметр
000 (3/0) размер 4,75 мм диаметр
00 (2/0) размер 4,5 мм диаметр
0 размер — 4,25 мм диаметр
1 размер — 4 мм диаметр
2 размер — 3,75 мм диаметр
3 размер — 3,5 мм диаметр
4 размер — 3,25 мм диаметр
5 размер — 3 мм диаметр
6 размер — 2,75 мм диаметр
7 размер — 2,5 мм диаметр
8 размер — 2,25 мм диаметр
9 размер — 2 мм диаметр
10 размер — 1,75 мм диаметр
11 размер — 1,50 мм диаметр
12 размер — 1,25 мм диаметр – самая мелкая дробь

Рубрики: Технологии умельцев

Онлайн калькулятор дробей. Вычисления с дробями. Сложение, вычитание, умножение и деление дробей.

Инструкция использования калькулятора дробей

Для решения вашей задачи выполните следующие действия:

• введите ваш пример в калькулятор;
• нажмите кнопку  для выполнения вычислений.

Ввод данных в калькулятор дробей

В калькулятор дробей можно вводить: целые числа, десятичные дроби, обыкновенные дроби и смешанные числа.

Целые числа. Для ввода целых чисел используйте цифровые клавиши калькулятора или цифровые клавиши вашего компьютера. 1 2 3 4 5 6 7 8 9 0

Десятичные дроби. Десятичные дроби вводятся также как и целые числа, в качестве десятичного разделителя рекомендуется использовать точку .

Обыкновенные дроби: Для ввода обыкновенной дроби нажмите клавишу на клавиатуре калькулятора — после чего введите значения числителя и знаменателя дроби используя числовые клавиши.

Смешанные числа: Используя числовые клавиши введите целую часть смешанной дроби, нажмите клавишу дроби на клавиатуре калькулятора — после чего введите значения числителя и знаменателя дроби используя числовые клавиши.

Отрицательные числа: Перед числом поставьте знак минус -, не забывайте брать отрицательные числа в скобки ( ).

Возведение в степень: Для возведения числа в степень введите число нажмите клавишу a^b, затем введите значение степени. (На компьютере степень можно ввести нажав клавишу «^». Например, для ввода 4³ нужно набрать 4^3)

N.B. Калькулятор поддерживает только целые степени!

N.B. Буквенные выражения, операции извлечения корня калькулятор не поддерживает!

Дополнительные возможности калькулятора дробей — старая версия

• С — полностью очистить поле ввода.
•  — удалить один символ.
•   для перемещения между полями калькулятора.